Rolling a cone on the plane
A right circular cone has a height of and a semi-vertical angle of (This is the angle between the axis of cone and any straight line on the surface of the cone passing through the apex). Initially, the cone is placed on the plane so that it tangent to both the and planes with its apex at the origin. Then, it is made to roll along the plane, as shown in the GIF animation below, till it becomes tangent to the plane. Find the area of the circular sector swept by the line segment of tangency between the cone and the plane.
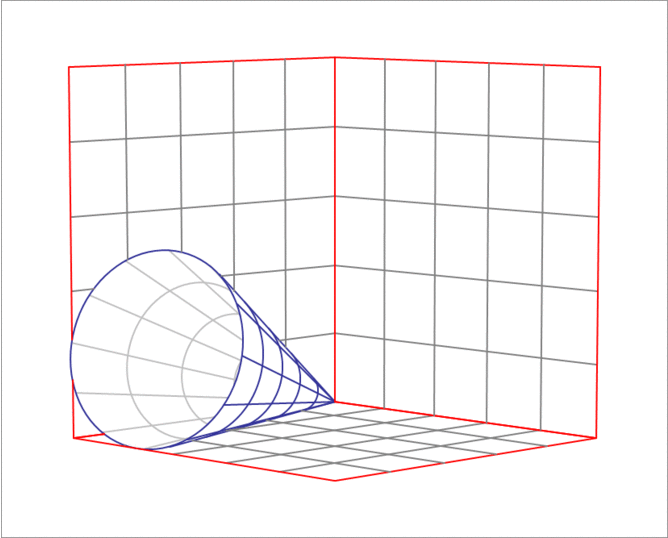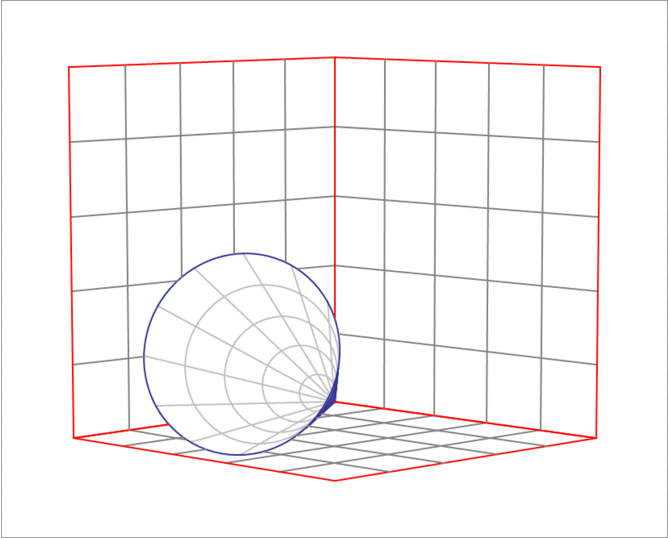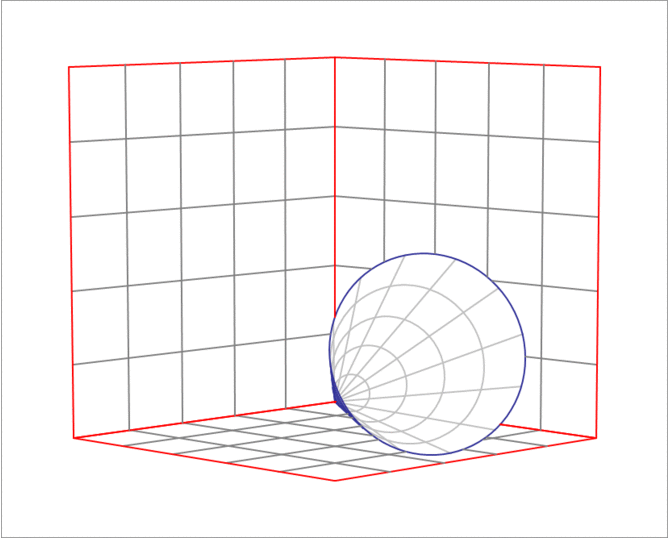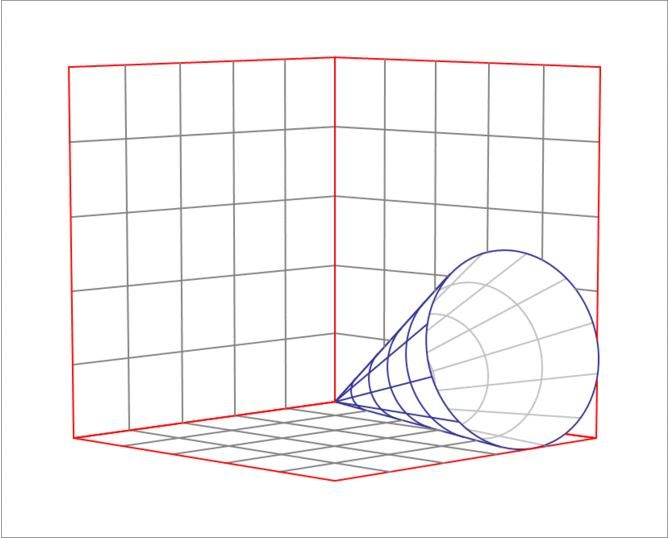
The answer is 123.9857.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider the cone in the initial position. We'll find the unit vector a along its axis. Since the semi-vertical angle is θ c = 1 5 ∘ , and the cone surface is tangent to the x y plane, then the axis makes an angle of θ c with the x y plane, and similarly it makes an angle of θ c with the x z plane. If k is the unit vector along the z -axis, then it follows that,
a ⋅ k = cos ( 2 π − θ c ) = sin θ c
And similarly, if j is the unit vector along the y -axis, then
a ⋅ j = cos ( 2 π − θ c ) = sin θ c
If the unit vector a = ( a x , a y , a z ) , then from the above equations,
a z = a y = sin θ c
And, since a is a unit vector, then a x = 1 − a y 2 − a z 2 = 1 − 2 sin 2 θ c = cos 2 θ c
The line segment of tangency between the cone and the x y plane has a length of the slant height of the cone, which is s = cos θ c h = cos θ c 1 5 and points along the projection of the cone's axis onto the x y plane, that is, along the vector ( cos 2 θ c , sin θ c ) , thus the initial angle that this tangency line segment makes with the x -axis is
ϕ 0 = tan − 1 cos 2 θ c sin θ c
Now from the symmetry of the problem, it follows that the final angle (with the x -axis ) is 2 π − ϕ 0 , Hence, the angle swept by the tangent line segment is Δ ϕ = 2 π − 2 ϕ 0 . So, finally, the area of the sector is
Sector Area = 2 1 s 2 Δ ϕ
And this evaluates to 1 2 3 . 9 8 5 7