Rolling a Parabola
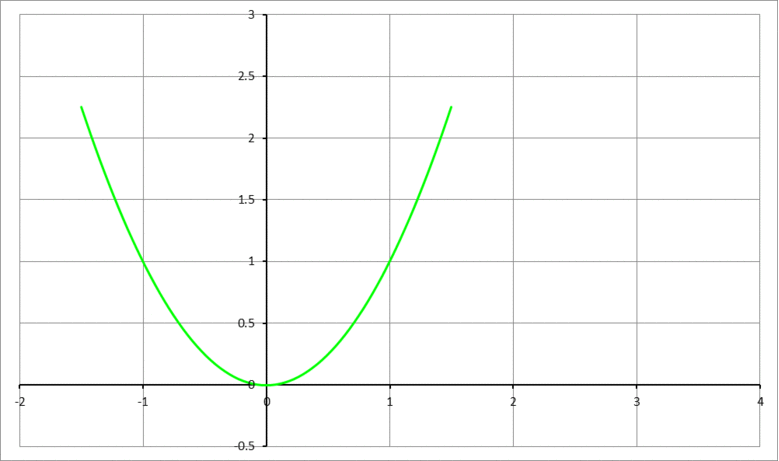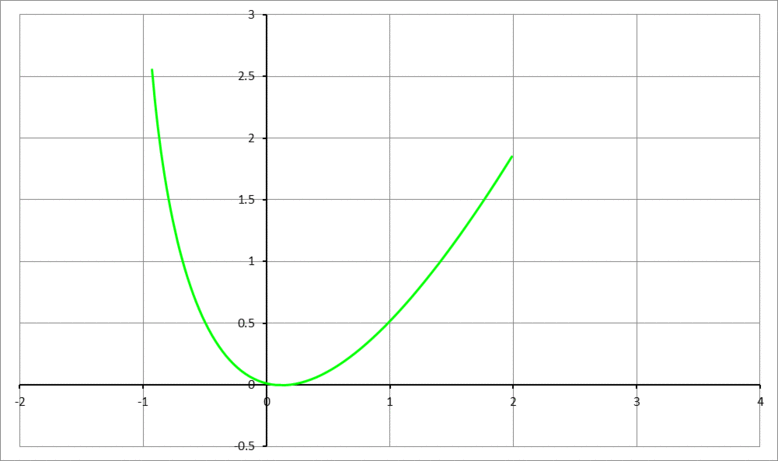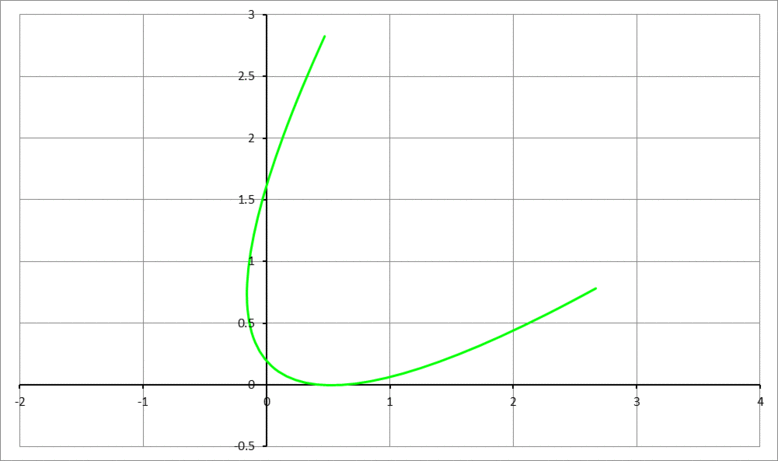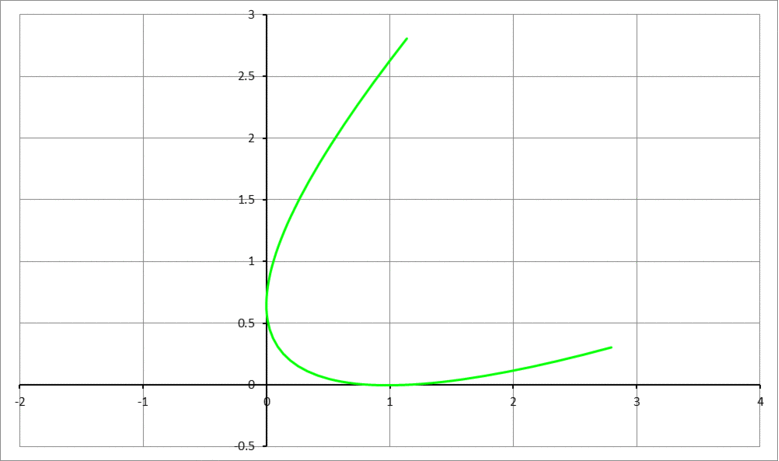
The animation above shows the parabola y = x 2 being rolled clockwise along the positive x -axis. Rolling stops when the rolled parabola becomes tangent to the y -axis. If ψ ∘ is the clockwise angle that the parabola was rolled through, and ( a , 0 ) and ( 0 , b ) are the tangent points of the final parabola with the x -axis, and the y -axis, respectively, then find the value of 1 0 a + 1 0 b + ψ . Note that the angle ψ must be expressed in degrees.
The answer is 72.8064794706532.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Excellent work.
We're given the parabola y = x 2 . We want to roll it such that it is always tangent to the x-axis. To that end, we have two coordinate frames: O x y which is the fixed reference frame, and O ′ x ′ y ′ which is rigidly attached to the rolling parabola and rolls with it. To relate the two frames, let r ′ be the position vector in O ′ x ′ y ′ of any point, and r be the position vector of the same point in O x y . Note that frame O ′ x ′ y ′ is rotated by an angle ψ ∘ clockwise, with respect to frame O x y . Further, the contact point has coordinates r 1 ′ = ( x 1 , x 1 2 ) in frame O ′ x ′ y ′ with a corresponding coordinate vector in O x y of r 1 = ( L , 0 ) . Hence, from the first observation, we have
r = R r ′ + d
where
R = [ cos ψ ∘ − sin ψ ∘ sin ψ ∘ cos ψ ∘ ]
Substituting the contact point, results in,
r 1 = R r 1 ′ + d
Substracting, and re-arranging, we get,
r = R ( r ′ − r 1 ′ ) + r 1
Now we need to specify angle ψ and L in terms of x 1 . It is straight forward to find that,
ψ = tan − 1 ( 2 x 1 )
and
L = ∫ 0 x 1 1 + 4 t 2 d t = 4 1 ( sec ψ tan ψ + ln ∣ sec ψ + tan ψ ∣ )
The other point of interest on the parabola, is the point r 2 ′ = ( x 2 , x 2 2 ) where the tangent is perpendicular to the tangent at ( x 1 , x 1 2 ) . It can be seen that x 2 = 2 − 1 cot ψ .
The corresponding absolute position vector in O x y is
r 2 = R ( r 2 ′ − r 1 ′ ) + r 1
In particular, the x-coordinate of r 2 is
r 2 x = x ∗ = L + cos ( ψ ) ( x 2 − x 1 ) + sin ( ψ ) ( x 2 2 − x 1 2 )
Note that L , x 1 and x 2 are functions of the angle ψ as defined above.
Finally, we want to solve for ψ that will result in x ∗ = 0 . That is, we want to find the root of x ∗ ( ψ ) . This can be done using Newton's method, as the derivative is readily available.
Doing so, results in
ψ ∘ = 5 6 . 4 6 5 8 3 5 1 2 7 4 5 2 3 ∘
a = L = 0 . 9 8 2 7 5 2 0 0 8 0 9 3 0 9 3
b = r 2 y = 0 . 6 5 1 3 1 2 4 2 6 2 1 5 8 9 1
This makes the answer,
1 0 a + 1 0 b + ψ = 7 2 . 8 0 6 4 7 9 4 7 0 5 4 2 2
Let ( c , c 2 ) denote the point on the graph of y = x 2 which then rolls to the point ( a , 0 ) .
The act of rolling the graph on the x -axis implies the following:
To find the equation of the graph after we roll it, we do the following, in order:
Note that the result will be a rotated graph such that the original point ( c , c 2 ) moves to the point ( a , 0 ) , which is exactly the same result as rolling the graph. Here are the results of each step:
By definition, this is the equation of the rolled parabola. Therefore, it has a vertical tangent at the point ( 0 , b ) , and algebraically, this just means that setting x = 0 in the equation will result in a quadratic with a repeated root at y = b . Following this, we set x = 0 : y 2 − y ( − c a + 4 c 2 ( 4 c 2 + 1 ) 3 / 2 ) + 4 c 2 a 2 = 0 . Then since it has a repeated root at y = b (and from the geometric picture, we know b > 0 ), it follows that b = 4 c 2 a 2 = 2 c a . Additionally, since the root is repeated , the discriminant of the quadratic equals zero: ( − c a + 4 c 2 ( 4 c 2 + 1 ) 3 / 2 ) 2 − 4 ⋅ 4 c 2 a 2 = 0 which simplifies to a = 8 c ( 4 c 2 + 1 ) 3 / 2 .
That's basically all we need! We have found that a = 8 c ( 4 c 2 + 1 ) 3 / 2 , b = 2 c a = 1 6 c 2 ( 4 c 2 + 1 ) 3 / 2 , ψ ∘ = tan − 1 ( 2 c ) and in order to solve for c , we can set the two equations we found for a equal to one another: 8 c ( 4 c 2 + 1 ) 3 / 2 = 2 1 c 1 + 4 c 2 + 4 1 sinh − 1 ( 2 c ) , which simplifies to 4 c 2 + 1 = 2 c sinh − 1 ( 2 c ) .
And.... well, that's as far as we can go algebraically. We probably could use some argument with the Lambert W function to find an exact form, but I honestly didn't bother with that. Instead, we can just solve it numerically to find c ≈ 0 . 7 5 4 4 3 9 7 8 0 7 6 9 1 5 9 9 6 4 4 5 4 9 4 2 2 4 4 0 8 0 2 8 9 2 8 6 8 4 7
Putting this into the equations for the other quantities: a ≈ 0 . 9 8 2 7 5 2 0 0 8 0 9 3 0 9 3 1 5 8 8 3 7 2 2 5 4 6 1 9 7 5 4 4 9 3 0 4 3 7 b ≈ 0 . 6 5 1 3 1 2 4 2 6 2 1 5 8 9 1 1 3 0 2 6 5 3 4 1 6 7 6 7 4 0 4 2 8 2 2 6 3 3 ψ ≈ 5 6 . 4 6 5 8 3 5 1 2 7 4 5 2 3 4 8 1 0 6 3 0 5 9 7 9 6 4 5 0 7 2 1 8 0 1 2 9 5 and putting it together: 1 0 a + 1 0 b + ψ ≈ 7 2 . 8 0 6 4 7 9 4 7 0 5 4 2 1 9 0 9 9 7 3 3 1 6 5 1 0 3 2 2 3 0 9 5 5 4