Rolling coin
A U.S quarter is rolling on the floor without slipping in such a way that it describes a circular path of radius R = 4 cm . The plane of the coin is tilted at an angle of θ = 4 5 ∘ with respect to the horizontal plane (see the figure below). Find the coin's period T in seconds , that is, the time it takes for the coin to go around the circle of radius R . The radius of a U.S quarter is r = 1 . 2 cm .
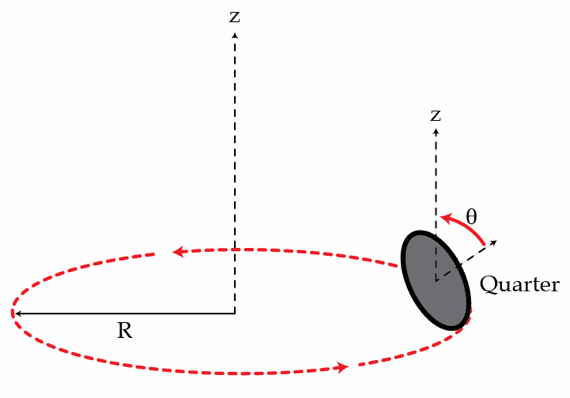
Details and assumptions
Assume g = 9 . 8 m/s 2 .
The answer is 0.446.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
http://physics.stackexchange.com/questions/72607/a-rolling-quarter
I didn't understand properly
Hey its a cheated solution from physicsstackechange...
You are right Louie T
interesting so r u 21 and in UMD study the quantum physic and then also 14 inside of India??? here is ali: http://groups.jqi.umd.edu/gorshkov/people/ali-hamed-moosavianexpected
more information of ali: http://physics.stackexchange.com/users/24791/ali
Obviously, the solution is copied. Who posted the problem on stack exchange anyways?
PS: Nice to know someone from the same city.
Perfect and clear !
Can you please explain how you wrote down the expression for omega
Hey everybody listen i'm not that kind of guy that's me only on stack exchange with my other name of Ali so that's only me here so please think before writing anything for anybody !!!
Log in to reply
should edit stack exchange post for some way to know is true
Damned big time..
Let us consider the triangle relating the base of the quarter, B , center of gravity of the quarter, G, and the center of the circle, C.
Note that angle GBC = 4 5 o due to the tilt of the quarter, and lengths B C and B G are R = 4 cm and r = 1 . 2 cm respectively. Hence, using cosine rule, length C G = 3 . 2 6 3 7 c m . Thereafter, using sine rule, angle GCB = 1 5 . 0 6 9 o
Now, we know that the centripetal acceleration required must be along line C G directed at an angle of 1 5 . 0 6 9 o from the horizontal.
Let us now consider the free body diagram of the coin. At the center of gravity, we have the acceleration due to normal contact force , a N , and the acceleration due to the weight of the coin g . a N is directed 4 5 o away from the horizontal. Now, we need to resolve the forces to produce one that is along line C G
We now set line CG as the new x-axis and its corresponding normal as y-axis, which this new set of orthogonal base tilted 1 5 . 0 6 9 o counter-clockwise. Now, the angle that g makes with the y-axis is 1 5 . 0 6 9 o and the angle that a N makes with the y-axis is 4 5 o − 1 5 . 0 6 9 o = 2 9 . 9 3 1 o
With that, resolving forces along y-axis,
a N c o s ( 2 9 . 9 3 1 o ) = g c o s ( 1 5 . 0 6 9 o ) ---- Equation (1)
Resolving along x-axis,
a c = a N s i n ( 2 9 . 9 3 1 o ) + g s i n ( 1 5 . 0 6 9 o ) --- Equation (2)
Hence, we can solve for a c
Using a c = r ω 2 , and ω = T 2 π ,
T = 0 . 4 4 4 s
Note : The answer might be slightly off due to round-off errors :X
It would be quite difficult to explain the answer to this question without images so i would be giving links to images I used for solving the question:
So a simplified figure for starting off with the solution: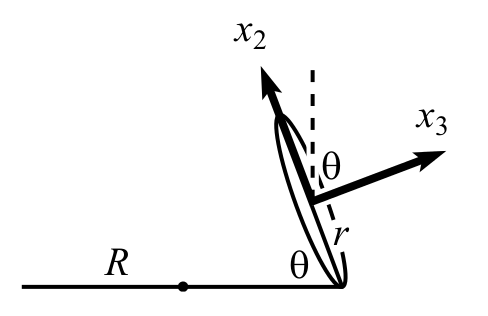
Let's first go to the CM frame. As it can be seen in the figure above, I will illustrate the principal axis by x 1 (into the page), x 2 and x 3 .
Let Ω be the angular velocity of the attaching point of the coin with the floor around the center. This means T = 2 π Ω .
Using the non-slipping condition, one will find out that the total angular momentum is:
ω = Ω z ^ − r R Ω x ^ 3
Now writing z ^ in the principal coordinates as sin θ x ^ 2 + cos θ x ^ 3 we will have:
ω = Ω sin θ x ^ 2 − Ω ( r R − cos θ ) x ^ 3
The principal moments are:
I 1 = I 2 = 4 m r 2 and I 3 = 2 m r 2
so the angular momentum will be:
L = 2 m r 2 ( 2 1 Ω sin θ x ^ 2 − Ω ( r R − cos θ ) x ^ 3 )
Only the horizontal component of L is changing:
∣ d t d L ∣ = Ω L ⊥ = 4 1 m r Ω 2 sin θ ( 2 R − r cos θ ) .
Now we have to calculate the torque relative to CM, as well. The torque comes from the forces at the contact point, the horizontal force is m ( R − r cos θ ) Ω 2 and the vertical force will be simply m g . :
∣ τ ∣ = m g ( r cos θ ) − m ( R − r cos θ ) Ω 2 ( r sin θ )
Using ∣ τ ∣ = ∣ d t d L ∣ , we can find:
Ω = 2 6 R tan θ − 5 r sin θ g
⇒ T = π g 6 R tan θ − 5 r sin θ ≈ 0 . 4 4 6 s