Rolling Cone
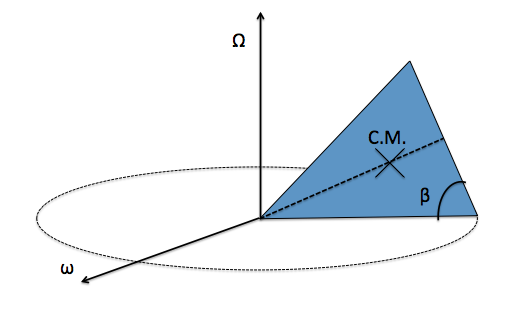
A rigid cone rolls on a very rough, horizontal surface (rough enough to prevent it from sliding) and its center of mass follows a circular trajectory.
Suppose the angular velocity of the center of mass of the cone is , and the angular velocity at which the cone rotates as seen by someone in the reference frame of the center of mass is .
What is the ratio of to ?
Note: The angle between the cone's base and slant height is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the slant height of the cone and the radius of the base of the cone be l and r respectively.
The circumference of the big circle is C = 2 π l , and the circumference of the base of the cone is c = 2 π r .
The center of mass of the cone takes time t = Ω 2 π to complete one revolution about the vertex of the cone. During this time, the point of contact between the cone and the ground moves a distance of 2 π l . This means that the circular base makes c C = r l revolutions, or rotates by 2 π r l radians.
This implies that the circular base is rotating with angular velocity Ω 2 π 2 π r l = r l Ω . However, we know that this is equal to ω . Thus, we can equate them:
ω = r l Ω ⟹ ω Ω = l r = cos β