Rolling Down the Slope I

Classical Mechanics Level 3

A ball of mass $m$ is rolling down a curved slope without slipping as shown in the diagram. The coefficient of static friction is $\mu_s$ . Assume the acceleration due to gravity is $-g\hat{y}$ .

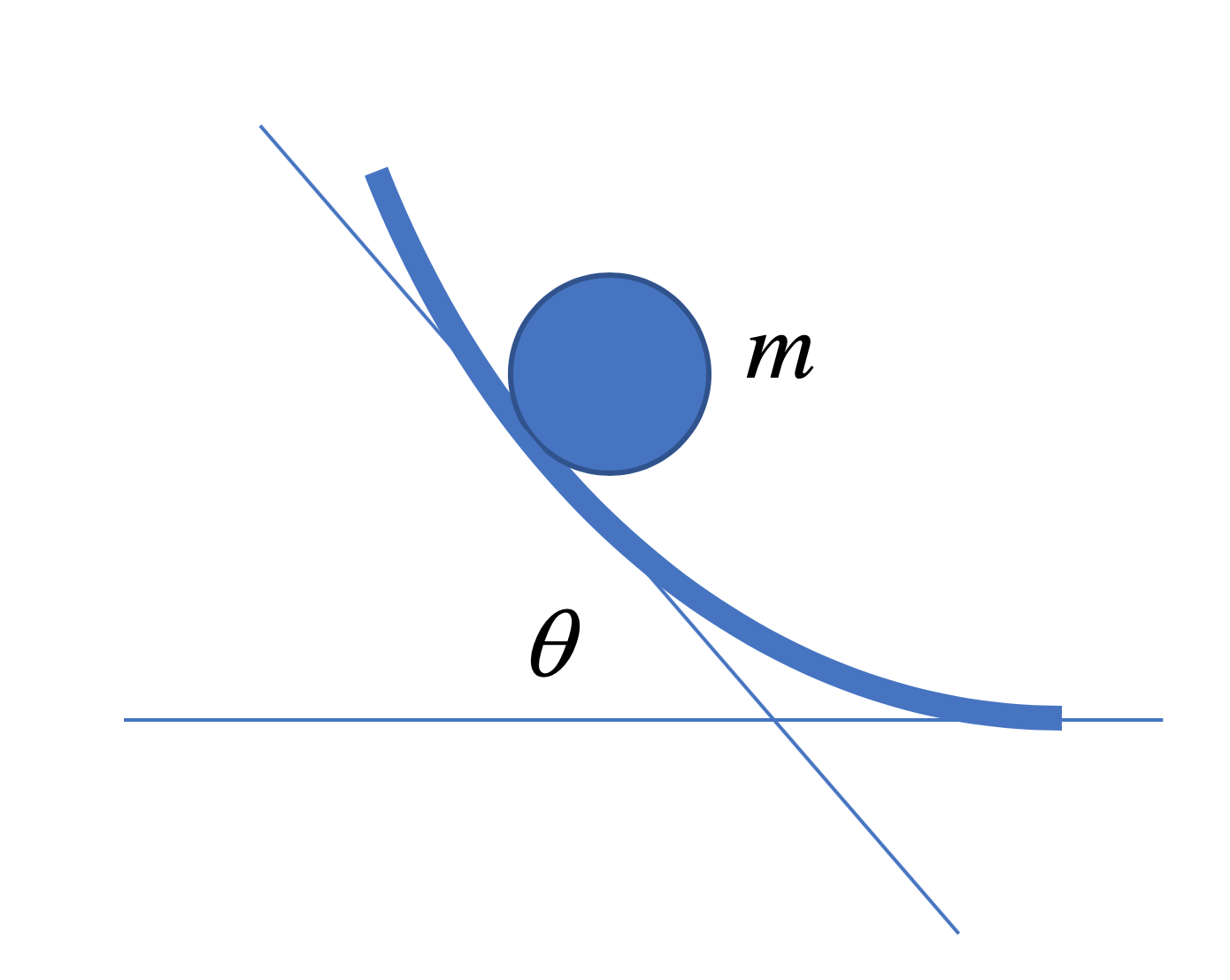
What can you say about the magnitude of the normal force acting on the ball?

hint: As indicated on the diagram, at any point on the slope, there's an equivalent incline with the same slope that makes an angle of $\theta$ with the horizontal.

N=mg\sin{\theta}

N=mg\cos{\theta}

N>mg\cos{\theta}

N<mg\cos{\theta}

1 solution

Max Yuen
Jun 8, 2019

In the diagram, if we drew the normal force acting on the ball and the normal component of the weight acting on the slope, we would get

$N-mg\cos{\theta} = ma_\perp$

Here $a_\perp$ is the acceleration in the normal direction. Without going in to the calculus details, we notice that the slope is negative but increasing (becoming more positive), meaning the tangent vector is turning left (or rotating counterclockwise). This is only possible if $a_\perp$ is positive. Thus, $N > mg\cos{\theta}$ .

We can also say it due to centrifugal force

Vishal S - 1 year, 5 months ago

Correct ... Centrifugal force adds to normal force which results in greater than normal.

Studentbxt bxt - 1 week, 4 days ago

That is exactly the point!

Max Yuen - 1 year, 3 months ago

Rolling Down the Slope I

1 solution

0 pending reports