Rolling Ellipse
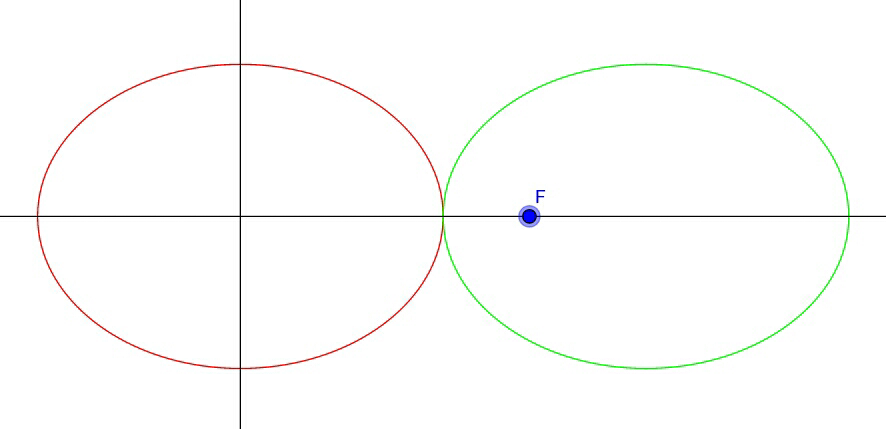 Consider an ellipse fixed at the origin of the
x
y
-plane having semi-major axis 4 and semi-minor axis 3.
A congruent ellipse rolls over the first ellipse without slipping. Initially, they share a common major axis.
Consider an ellipse fixed at the origin of the
x
y
-plane having semi-major axis 4 and semi-minor axis 3.
A congruent ellipse rolls over the first ellipse without slipping. Initially, they share a common major axis.
Find the locus of focus (the one nearer to the origin) of the rolling ellipse, and calculate the distance traveled by the focus in one revolution (around the fixed ellipse), to 3 decimal places.
The answer is 50.265.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
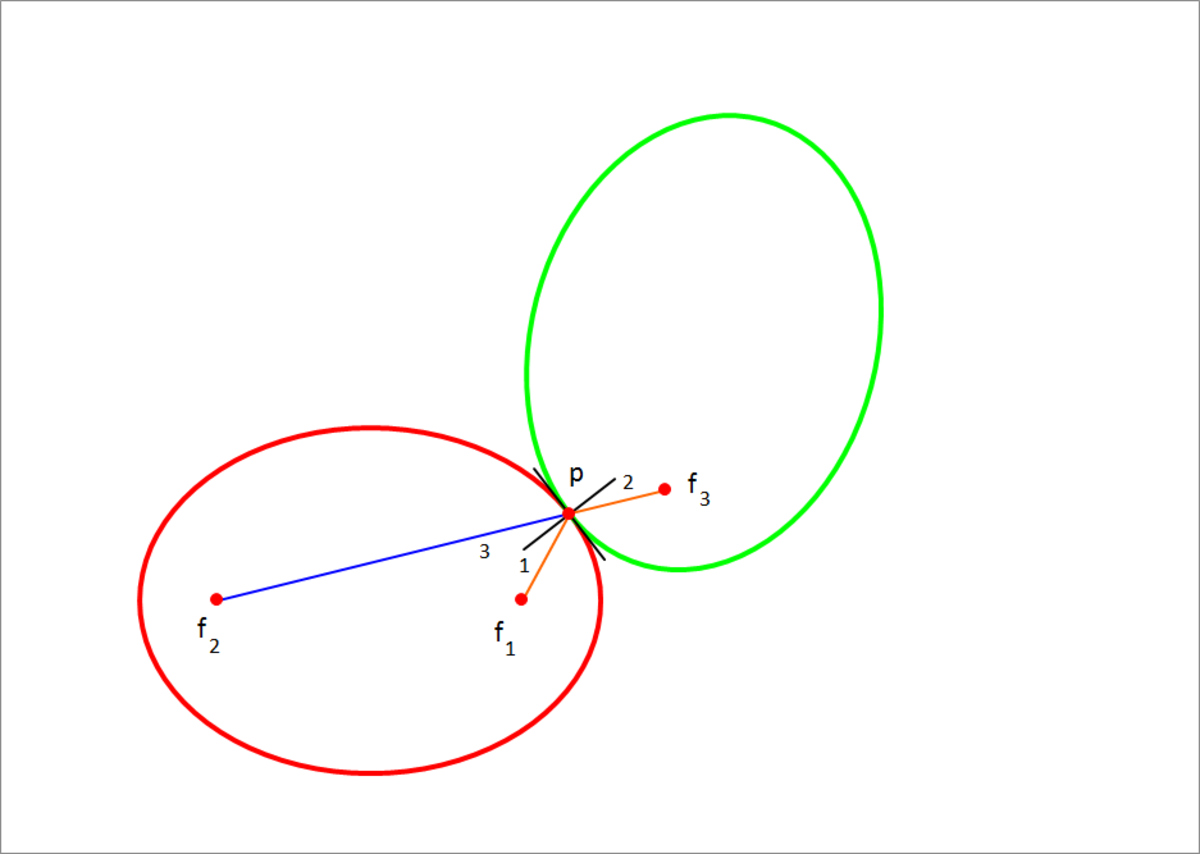
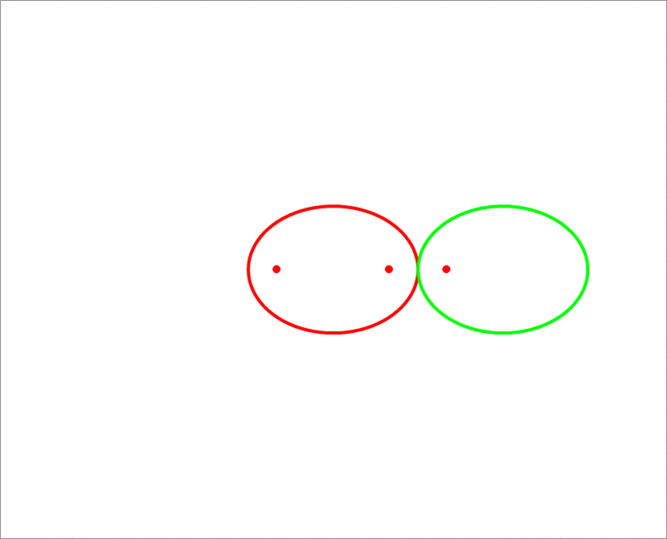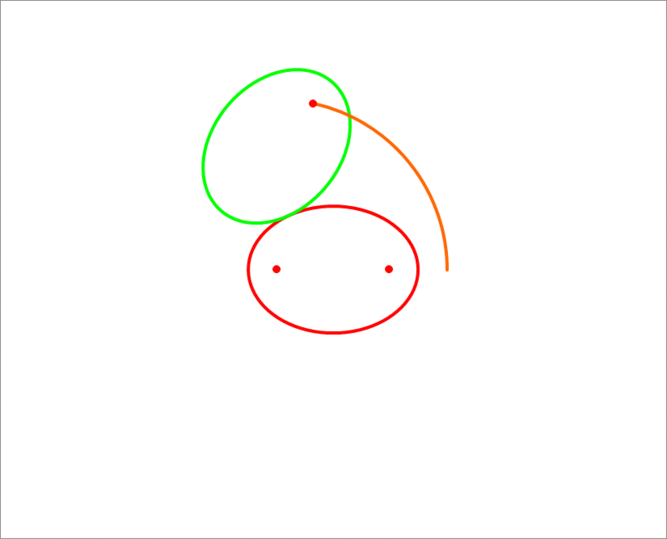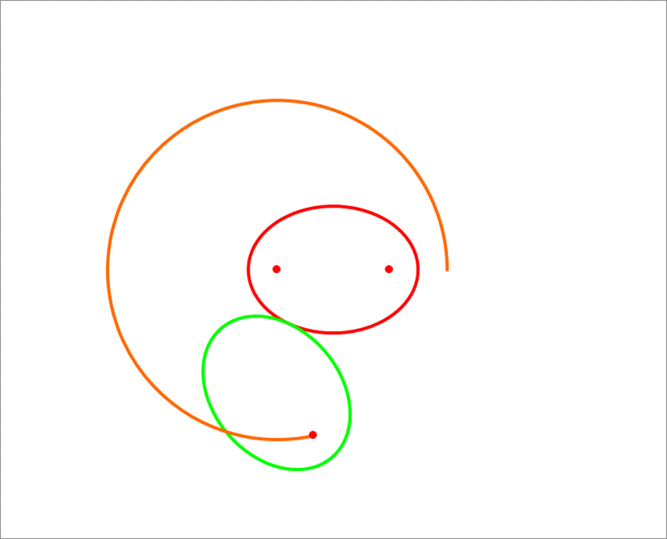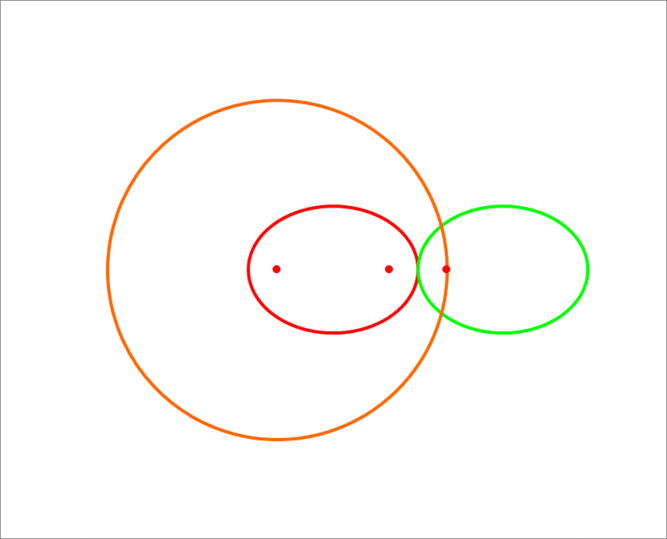
As the two ellipses are congruent, it follows that the rolled ellipse and the fixed ellipse are mirror images about the common tangent. Hence ∠ 1 = ∠ 2 . Also we know from the properties of ellipses that the normal at any point on the ellipse bisects the angle between the line segments connecting the point to the two foci. Hence ∠ 1 = ∠ 3 . From this, it follows that the points p , f 2 and f 3 are collinear. Further, we know that the sum of p f 3 + p f 2 = p f 1 + p f 2 = 2 a , where a is the semi-major axis length. Hence the focus of the rolling ellipse is at a constant distance equal to 8 from the left focus of the fixed ellipse. Therefore, the locus is a circle with radius equal to 8 , from the which the length is the circumference of this circle which is equal to 1 6 π = 5 0 . 2 6 5 .
The following GIF image shows the trajectory of the rolling ellipse focus.
Great solution!!!!...... How do you draw such animations? @Hosam Hajjir
Log in to reply
I used Excel VBA.
@Aaron Jerry Ninan Solved! :D
I bashed it with coordinates that finally led to the simple equation of circle that was so easy to see using elementary properties. :( :(
The locus of the focus will be a circle having radius 2 a and centre at ( − a 2 − b 2 , 0 ) .