Rolling in a cone

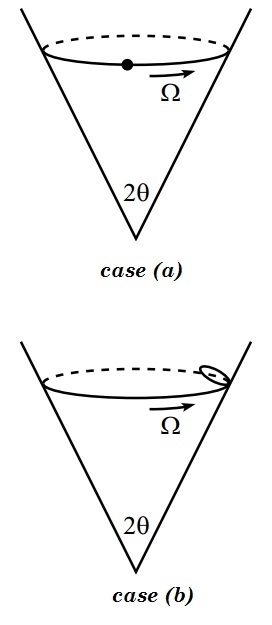(a) A fixed cone stands on its tip, with its axis in the vertical direction. The half-angle at the vertex is $\ θ$ . A particle of negligible size slides on the inside frictionless surface of the cone (see case(a)). Assume conditions have been set up so that the particle moves in a circle at height $\ h$ above the tip.
Let the frequency of this circular motion be $\ Ω_a$ .

(b) Assume now that the surface has friction, and a small ring of radius $\ r$ rolls without slipping on the surface. Assume conditions have been set up so that (1) the point of contact between the ring and the cone moves in a circle at height $\ h$ above the tip, and (2) the plane of the ring is at all times perpendicular to the line joining the point of contact and the tip of the cone (see case(b)). You may work in the approximation where $\ r$ is much less than the radius of the circular motion, $\ h tanθ$ . Let the frequency of this circular motion be $\ Ω_b$ .

Question: Find $\frac{Ω_a}{Ω_b}$ .