Rolling Rugby

Calculus Level 2

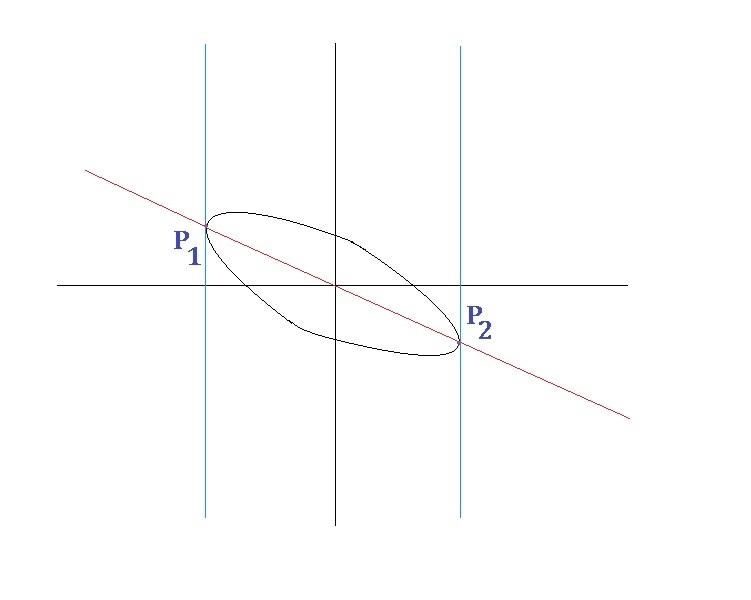
As shown above is the elliptical graph of $x^2 + xy + y^2 = 7$ , where $P_{1}$ and $P_{2}$ are the points on the graph with minimum and maximum $x$ coordinates respectively, and the red line $l$ is the linear graph passing through $P_{1}$ and $P_{2}$ .

If the tangent parallel to line $l$ touches the graph at a point $P_{3} (a,b)$ for some real numbers $a,b$ , compute $a^2 + b^2$ .

The answer is 7.

1 solution

Worranat Pakornrat
Jul 28, 2016

By using implicit differentiation, we can evaluate f'(x) as shown below:

$x^2 + xy + y^2 = 7$

$\dfrac{d(x^2 + xy + y^2)}{dx} = 0$

$2x + (y + x f'(x)) + 2y(f'(x)) = 0$

$f'(x)(x + 2y) = - (2x + y)$

$f'(x) = \dfrac{-(2x + y)}{x + 2y}$

The slope of the blue lines touching $P_{1}$ & $P_{2}$ reaches infinity as in terms of $f'(x)$ . This occurs when the denominator $x + 2y = 0$ or $y = \dfrac{-x}{2}$ , which is the equation for the red line. In other words, the red line $l$ has a slope of $\dfrac{-1}{2}$ .

Now for the tangent of slope $\dfrac{-1}{2}$ , we can plug in this value to $f'(x)$ :

$f'(x) = \dfrac{-(2x + y)}{x + 2y} = \dfrac{-1}{2}$

$x + 2y = 4x + 2y$

$3x = 0; x = 0$

The tangent touches the graph when $x = 0$ , and we can calculate for y-value as $y^2 = 7$ .

As a result, $a^2 + b^2 = 0 + 7 = \boxed{7}$ .

Rolling Rugby

The answer is 7.

1 solution

0 pending reports