Rolling Sphere on a plank with Pulley

The rolling requires a static friction force $F_f$ , which acts to the right on the sphere and to the left on the block. However, because of the way the pulley is set up, both friction forces oppose the acceleration of the system. From Newton's Second Law, we have $(M + m)a = \SI{40}{N} - 2F_f,$ where $M$ , $m$ are the mass of the block and the sphere, respectively.

To obtain rolling motion, the rotational acceleration of the sphere must match the linear acceleration relative to the block . This gives $\alpha = \frac{2a}r.$ Working out the details of torque due to friction and rotational inertia, $F_f = \frac{\tau}r = \frac{I\alpha}r = \frac{\tfrac25mr^2\cdot 2a/r}r = \tfrac45 ma.$ Thus $(M + m)a = \SI{40}{N} - \tfrac85 ma, \\ a = \frac{\SI{40}{N}}{\SI{5 + 3 + 4.8}{kg}} = \boxed{\SI{3.125}{m/s^2}}.$

Analysis of forces

On the 5-kg block act

• 40 N of pulling force to the right

• 7.5 N of friction force to the left

• 16.875 N of tension force to the left

• for a total net force of 15.625 N to the right.

On the 3-kg block act

• 7.5 N of friction force to the right

• 16.875 N of tension force to the left

• for a total net force of 9.375 N to the left.

Energy analysis

No dissipative forces act on the system; static friction converts translational motion into rotational motion without energy losses. The only external work on the system is the pulling force of 40 N.

Suppose the block (mass $M$ ) is sliding at speed $v$ . Then the sphere (mass $m$ ) has the same speed in opposite direction; its speed relative to the block is $2v$ , and the rotation of the sphere satisfies $2v = r\omega$ . Therefore the kinetic energy of the system is $K = \tfrac12Mv^2 + \tfrac12mv^2 + \tfrac12I\omega^2 = \tfrac12(M + \tfrac{13}{5}m)v^2.$ (The rotational inertia of the sphere is $I = \tfrac25mr^2$ , so that $I\omega^2 = \tfrac25mr^2(2v/r)^2 = \tfrac85mv^2$ .)

In time $dt$ , the 40-N pulling force acts over a distance $dx = v\:dt$ doing $dW = Fv\:dt$ of work. This is the increase in the system's kinetic energy: $dK = dW$ . Thus $(M + \tfrac{13}{5}m)v\:dv = Fv\:dt,$ showing that $a = \frac{dv}{dt} = \frac{F}{M + \tfrac{13}5 m} = \frac{\SI{40}{N}}{\SI{5 + 7.8}{kg}} = \boxed{\SI{3.125}{m/s^2}}.$

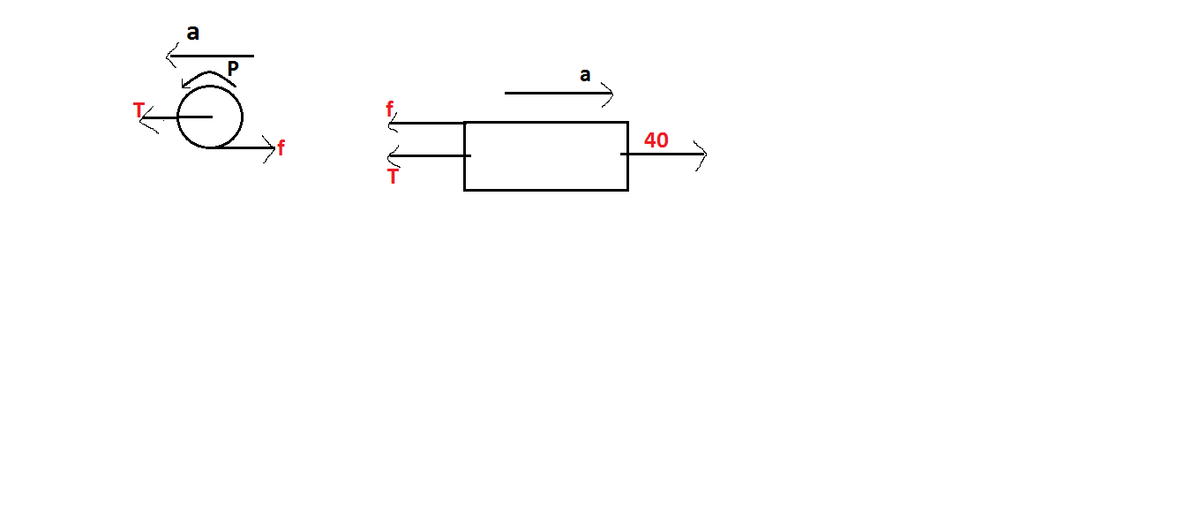
T = Tension

f = friction

a = acceleration

p = angular acceleration

The acceleration of block as well as of sphere will be same because they are connected with a single string.

Friction will be acting in backward direction of sphere otherwise the sphere would have slipped.

$T - f = 3a$

$40 - T - f = 5a$

Let R be the radius of the sphere.

$R*p - a = a$ [No slipping condition]

$f.R = \frac{2*(3*R^2)*p}{5}$ [Torque]

Solving these equations $a = 3.125 m / s^2$

Let's first define some variables as follows:

$\alpha$ = Angular acceleration of sphere

$a$ = Acceleration of plank

$f$ = frictional force

$T$ = Tension the string

According to the given situation the following equations follow:

$\alpha*r-a=a \implies \alpha*r=2a$

$f*r=\dfrac{2}{5}mr^2 \alpha$

$40-f-T=5a$

$T-f=3a$

Solving the above equations we get :

$a=\dfrac{25}{8}$

Let us denote: M = mass of the plank, m = mass of the sphere, $F_f$ = frictional force, T = tension of the string, a = acceleration of the plank, R = radius of the sphere, $\beta$ = rotational acceleration of the sphere.

It is a problem on classical mechanics, so one should use Newton's laws and kinematic equations. We write Newton's second law for each of the bodies and account for the kinematic relation.

1. The plank: translational motion $Ma = F - T - F_f$ .

2. The sphere:

• translational motion: $ma = T - F_f$ ,

• rotational motion: $\frac{2}{5} m R^2 \beta = F_f R$ (relative to the horizontal axis through the sphere center), note that we use the expression for the moment of inertia of a solid sphere.

Kinematic relation: $2a = \beta R$ , for when one moves the plank to the right by $x$ , it means that the sphere rolls correspondingly to the left by $x$ relative to the plank. And here the sphere moves to the left by another $x$ due to the motion of the string. These $2x$ equal the length of the arc $\alpha R$ . In order to get the final kinematic relation one has to differentiate this equation twice.

Now we have the four equations with the four unknown variables $T, F_f, \beta, a$ . One can easily solve this system of equations and get $a = \frac{F}{M + 2.6m} = 3.125$ .

Since no energy is dissipated, the easiest way is to consider the total kinetic energy. We have $E=\frac12(m_{plank}+m_{sphere})v^2 +\frac12Iω^2$ where $I=\frac25m_{sphere} r^2$ and $ω=2v/r$ , so that $E=\frac{32}{5}v^2$ This corresponds to the energy $E=\frac12mv^2$ of an effective mass $m_{eff}= \frac{64}{5}$ , so that $a=F/m_{eff}=40×\frac{5}{64}=\frac{25}{8}=\boxed{3.125} \text{ } m/s^2$