Rolling Squares

Initial Position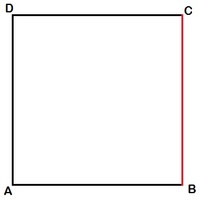

Rotation 1 $BC$ as handle, moves through a right angle. Distance covered by C is the arc length subtended by handle $BC$ , i.e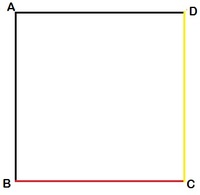. $\frac{\pi}{2}$

Rotation 2 $CD$ as handle, moves through an right angle. But C doesn't move from its position. So in this case, distance covered by C is 0.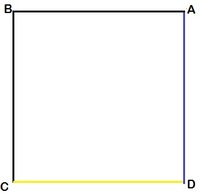

$$

Rotation 3 $DC$ as handle, moves through an right angle.Distance covered by C is the arc length subtended by handle $DC$ , i.e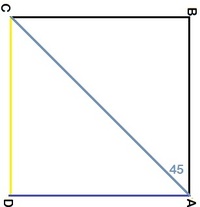. $\frac{\pi}{2}$

Rotation 4 As given in the last figure, the new handle is diagonal $AC=\sqrt{2}$ . In the 4th rotation, $AC$ moves through a right angle since angle BAC is $45^{\circ}$ and then angle $DAC$ is $45^{\circ}$ too. Hence $AC$ moves through a total of $45^{\circ}+45^{\circ}=90^{\circ}$ . In this case, distance covered by C is the arc length subtended by $AC$ i.e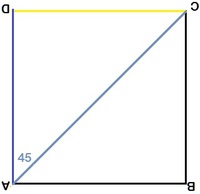. $\frac{\sqrt{2}}{2} \pi$

So, adding up the distances covered by C in the 4 rotations, we have $\frac{\pi}{2}+0+\frac{\pi}{2}+\frac{\sqrt{2}}{2} \pi=\boxed{(1+\frac{\sqrt{2}}{2}) \pi}$