This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Thanks, I've updated the answer.
Hah! You must be kidding me! This is by far the most easiest sum I have encountered here on Brilliant. Just use the Vieta's formula to find the product of the roots for the quadratic polynomial.
If roots are α , β , then,
\Large \alpha + \beta = \frac{-\text{Coefficient of x}}{\text{Coefficient of x^2}}
and, \Large \alpha. \beta = \frac{\text{Constant term}}{\text{Coefficient of x^2}}
ok..thanks a lot
roots of equation are 4,1 so product is 4
after factorization the two roots are (2-i) & (2+i) therefor the product of them is 4-i^2 and since i^2=-1 therefore 4-i^2 = 5
thnaks for your good contribution
Thank you!
Vieta's Formulas: x1 + x2 = -b/a x1*x2=c/a
The answer is correct, it's -5
multiplication of root is c/a
C/A =products of zero Hence ans =5/1
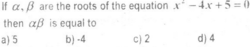
The answer must be 5. Product of roots=c/a=5