Root of unity problem for wiki
Let z be a 7 th root of unity . In other words, z is a complex number that satisfies the equation z 7 = 1 .
If z = a + b i , where a and b are real numbers, then what is the maximum value of a + b ?
Give your answer to 3 decimal places.
The answer is 1.40532128432676.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I had a similar line of reasoning with the addition that the angle could be in the third quadrant as well. This way we could look for the largest negative sum. It still turns out to be your answer but we could interpret the problem to include negative values as well.
 a
+
b
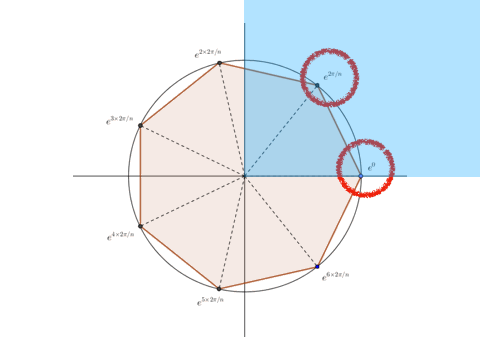
will be maximized when the 7th root is in the first quadrant. Thus we only have to check for these two values. Using euler's formula: \[\begin{align} e^{2\pi i} &= cis(2 \pi) = 1 + 0i & \implies a + b = 1
a
+
b
will be maximized when the 7th root is in the first quadrant. Thus we only have to check for these two values. Using euler's formula: \[\begin{align} e^{2\pi i} &= cis(2 \pi) = 1 + 0i & \implies a + b = 1
\\ e^{2\pi i / 7} &= cis\bigg(\frac{2 \pi}{7}\bigg) \approx 0.6234 + 0.7818i & \implies a + b \quad \approx 1.405 \end{align}\] The greater value is obtained at the second root with a + b = 1 . 4 0 5
We can have 7 values of z . So, using roots of unity, we have that: ⟹ z = e ( 2 π / 7 ) ⋅ i e ( 4 π / 7 ) ⋅ i e ( 6 π / 7 ) ⋅ i … , e ( 1 4 π / 7 ) ⋅ i
Now test all of these values, and use Euler's Formula, to see that our largest value will be around: ≈ 1 . 4 0 5
Relevant wiki: Roots of Unity
The 7 th roots of unity can be found with:
z = e 2 k π i / 7 for k = 1 , 2 , 3 , 4 , 5 , 6 , 7
The goal is to maximize a + b , so the angle 7 2 k π should either be in the first quadrant of the complex plane , on the Positive Real Axis, or on the Positive Imaginary Axis.
The only angles that meet this criteria are 2 π and 7 2 π .
Using Euler's Formula : e 2 π i = cos ( 2 π ) + i sin ( 2 π ) = 1 + 0 i e 2 π i / 7 = cos ( 7 2 π ) + i sin ( 7 2 π ) ≈ 0 . 6 2 3 4 9 + 0 . 7 8 1 8 3 i
It is clear that the root of unity that corresponds to the angle 7 2 π maximizes the value of a + b .
The maximum value is a + b ≈ 0 . 6 2 3 4 9 + 0 . 7 8 1 8 3 = 1 . 4 0 5 3 2 .