Rooting squares, squaring telescopes, telescoping roots...
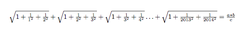 In the above equation, it is known that a, c, and b are 3 consecutive positive integers with
. What is the value of
?
In the above equation, it is known that a, c, and b are 3 consecutive positive integers with
. What is the value of
?
The answer is 2014.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 + n 2 1 + ( n + 1 ) 2 1 = n ( n + 1 ) n 4 + 2 n 3 + 3 n 3 + 2 n + 1 = n ( n + 1 ) n 2 + n + 1 = n + n 1 − n + 1 1 Then calculate the sum and take a = n , c = n + 1 and b = n + 2