Roots got mad!
Let x be a real positive number in the interval 6 1 5 3 ≤ x ≤ 6 3 9 8 . The maximum value of x − 1 + 2 x − 5 1 + 1 9 9 − 3 x is s and obtained when x = t . Find s + t .
For more problems on finding maximum and minimum value, click here
Try another problem on my new set! Warming Up and More Practice
The answer is 71.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Good solution!
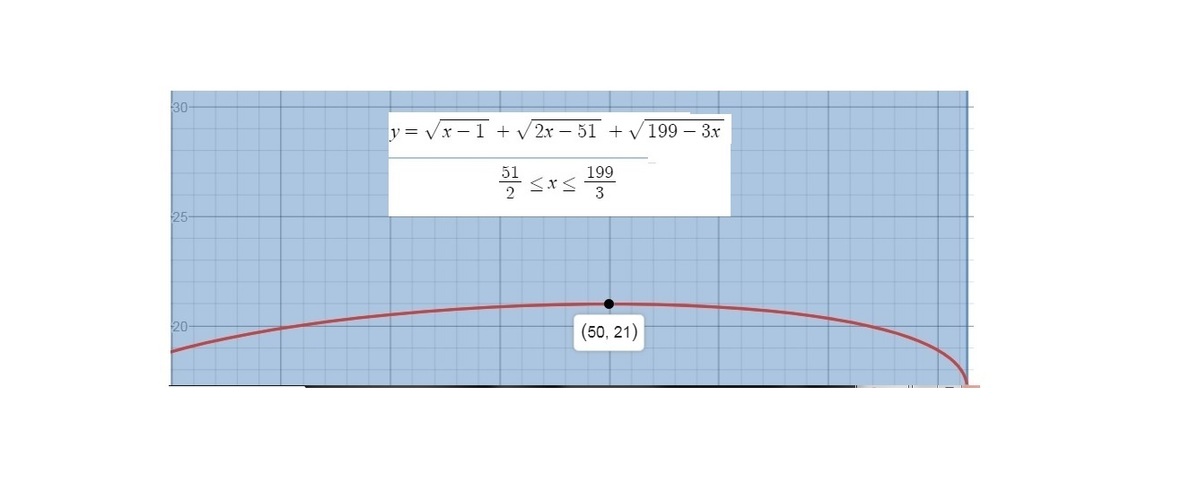L
e
t
f
(
x
)
=
x
−
1
+
2
x
−
5
1
+
1
9
9
−
3
x
.
W
i
t
h
i
n
t
h
e
r
a
n
g
e
,
f
o
r
m
a
x
x
=
t
=
5
0
.
.
.
.
.
.
.
.
.
.
y
=
f
(
5
0
)
=
s
=
2
1
.
∴
t
+
s
=
7
1
.
By Cauchy-Schwarz Inequality, we have,
[ ( x − 1 ) + ( 2 x − 5 1 ) + ( 1 9 9 − 3 x ) ] ( 1 + 1 + 1 ) 1 4 7 × 3 2 1 ≥ ( x − 1 + 2 x − 5 1 + 1 9 9 − 3 x ) 2 ≥ ( x − 1 + 2 x − 5 1 + 1 9 9 − 3 x ) 2 ≥ ( x − 1 + 2 x − 5 1 + 1 9 9 − 3 x )
Hence, s = 2 1 .
Equality holds when x − 1 = 2 x − 5 1 = 1 9 9 − 3 x .
Hence, x = 5 0 = t .
Making the answer s + t = 2 1 + 5 0 = 7 1 .