Roots power !
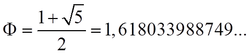 Calculate
(
2
1
+
5
)
1
6
+
(
2
1
−
5
)
1
6
Calculate
(
2
1
+
5
)
1
6
+
(
2
1
−
5
)
1
6
The answer is 2207.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let a = ( 2 1 + 5 ) , b = ( 2 1 − 5 ) then a + b = 1 and a b = − 1 next a 2 + 2 a b + b 2 = 1 therefore a 2 + b 2 = − 1 doing this step many times we'll get the answer a 1 6 + b 1 6 = 2 2 0 7
By Binet's formula for Lucas numbers, ϕ n + ( 1 − ϕ ) n = L n where L n is the n th Lucas number. Therefore we are looking for L 1 6 . L 1 6 = 2 2 0 7 If you are unfamiliar with the Lucas numbers, here is the basic definition: L 1 = 1 , L 2 = 3 , L n = L n − 1 + L n − 2 In other words, the first two numbers are 1 and 3 , and every number after that is the sum of the previous two numbers. They are very closely related to the much more popular Fibonacci sequence, and you can even calculate L n by adding F n − 1 + F n + 1 .