Rooty Pentagon

Note that $\begin{aligned} f(2z) &= 32(z^5 + z^4 + z^3 + z^2 + z + 1) \\ &= 32\left( \dfrac{z^6-1}{z-1} \right) \end{aligned}$ whose roots are all 6th roots of unity except $z=1$ . Now, if $r$ is a root of $f(2z)$ , then $2r$ is a root of $f(z)$ , so the roots of our original polynomial $f(z)$ are twice all the roots of $f(2z)$ , namely $2e^{i\frac{2k\pi}{6}}$ for $k = 1,2,3,4,5$ . On the complex plane, this appears as:

The rectangle has width $2$ and height $2\sqrt{3}$ , and the triangle has base $2\sqrt{3}$ and height $1$ , so their combined area is: $2 \cdot 2\sqrt{3} + \frac{1}{2} \cdot 2\sqrt{3} \cdot 1 = 5 \sqrt{3}$ So $a = \boxed{5}$

$\begin{aligned} z^5 + 2z^4+4z^3+8z^2+16z+32 & = 0 \\ (z+2)(z^4 + 4z^2+16) & = 0 \\ (z+2)(z^2+2-2\sqrt 3i)(z^2+2+2\sqrt 3i) & = 0 \\ (z+2)\left(z+1+i\sqrt 3\right)\left(z-1-i\sqrt 3\right)\left(z+1-i\sqrt 3\right)\left(z-1+i\sqrt 3\right) & = 0 \end{aligned}$

$\implies z = \begin{cases} 1+i\sqrt 3 & = 2e^{\frac \pi 3 i} \\ -1+i\sqrt 3 & = 2e^{\frac 23 \pi i} \\ -2 & = 2e^{\pi i} \\ -1-i\sqrt 3 & = 2e^{\frac 43 \pi i} \\ -1+i\sqrt 3 & = 2e^{\frac 53 \pi i} \end{cases}$

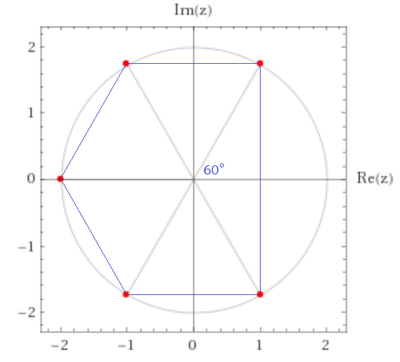
Plotting the roots on a complex plane, we note that the area of the pentagon is equal to five equilateral triangles with side length $2$ , which is $5 \times \frac 12 \times 2^2 \sin 60^\circ = 5\sqrt 3$ , therefore $a=\boxed 5$ .

factorizing the equation we get (x+2)(X^4+4x^2+16)=0 whose roots are -2,2w,-2w,2w^2,-2w^2 , where "w" is the complex cube root of unity. now simply plotting these points in the argand plane and finding the area using basic geometry ..