Rope and Brain
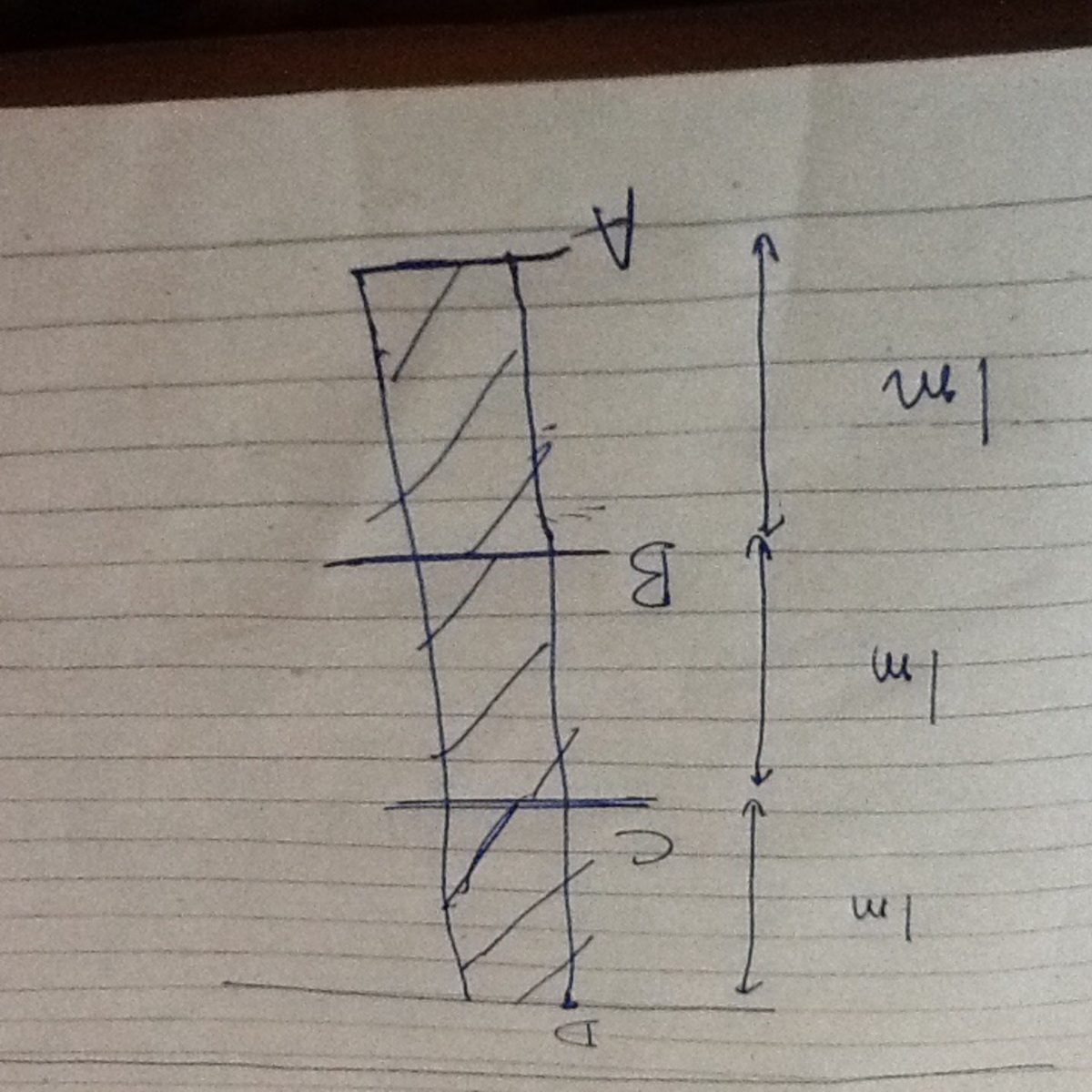
In the above you can see a rope whose mass is given by the equation
2M^2*(x)
, where M = 1 kg, and x is the distance from point
A
. Find the tension at the string on:-
(1.) Point
B
(2. ) Point
D
, but for this case x is the distance from point
B
, and below point
B
the mass of the whole string is given by
2M^2
.
(TAKE g to be 10ms^-2)
Find Z+ Y ( where Z is the answer for first part and Y for the second one). ( In your final answer which you choose from the options given, dont include 'N')
NOTE : POINT D IS THE BASE NOT POINT A . THE PICTURE IS INVERTED. SORRY FOR THE INCONVENIENCE
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
we can see that the mass of the string here, depends upon x. so we can write:- dm/dx [which means mass of a small piece of thread w.r.t to x )= 2M^2*( x )
=> dm = [2M^2*( x )]dx
integrating this equation, we get m=M^2*( x^2 ) ..............(1)
hence taking out the mass on point B , we use the above the above equation. (where x =1, and M is constant =1 kg)
we get, => m = (1^2)(1^2)=1
as tension is force, and we know F=ma
we infer tension = (1) *g = 10N
For the second part we know =>
{the mass of string from ( A to B ) + mass of string from ( D _ to _C )}* g = Tension
we know mass of string A to B is given by 2M^2= 2(1kg)=2kg
(NOTE: But here x is the distance from B not A )
so we get => m( DB )= (M^2)*( x )^2
hence we conclude total mass for part 2 is (4+2)kg =6kg
therefore tension = mg
=> T = (6)(10)N = 60 N
As the question asked the sum of the answers of the two parts, our final fnal answer comes out to be :-
60N + 10N =70N
plus we are also told to exclude 'N' in our final answer. Therefore the correct option is 70.