Rope between inclines
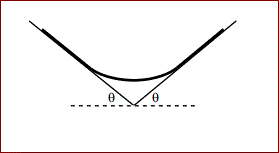 A rope rests on two platforms which are inclined at an angle
(which you are free to pick, as shown. The rope has uniform mass density, and its coefficient of friction with the platforms is 1.The system has left right symmetry. What is the largest possible fraction of the rope that does not touch the platforms ?
A rope rests on two platforms which are inclined at an angle
(which you are free to pick, as shown. The rope has uniform mass density, and its coefficient of friction with the platforms is 1.The system has left right symmetry. What is the largest possible fraction of the rope that does not touch the platforms ?
The answer is 0.172.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the rope have total length l , the hanging portion have length x , the coefficient of static friction be μ . We wish to maximize x / l .
There are 5 forces that act on the rope: 2 normal forces N , two static friction forces f , and the gravitational force. The forces balance in horizontal direction due to symmetry. In the vertical direction, 2 N c o s θ + 2 f s i n θ = m g 2 N ( c o s θ + μ s i n θ ) ≥ m g .
The normal force comes solely from the portion resting on the platform. The length of rope on either platform is 2 l − x , so N = 2 l − x l m g c o s θ .
Substituting into inequality, we have x / l ≤ 1 − ( c o s θ ( c o s θ + μ s i n θ ) ) − 1 , which has minimum 0 . 1 7 2 at θ = π / 8 .