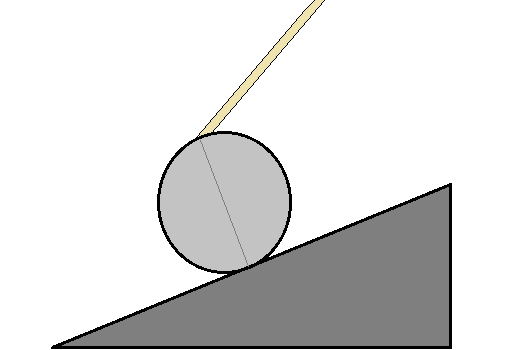
Rope Holding Sphere in Place

A sphere of mass $M$ and radius $R$ is held statically in place on a ramp by a rope pulling in the direction of the vector $\vec{v} = (1,2)$ . The anchor point for the rope is diametrically across from the contact point between the sphere and the ramp.

The ramp makes an angle $\theta$ with the horizontal, and there is a friction force between the sphere and the ramp surface.

If $T$ , $N$ , and $F$ are the magnitudes of the rope tension, the normal reaction force at the ramp, and the friction force at the ramp, determine $T + N + F$ .

Details and Assumptions:
- Downward gravity $g = 10 \, \text{m/s}^2$
- $M = 50 \, \text{kg}$
- $R = 1 \, \text{m}$
- $\theta = \large{\frac{\pi}{6}} \, \text{rad}$