Rope On Cylinder
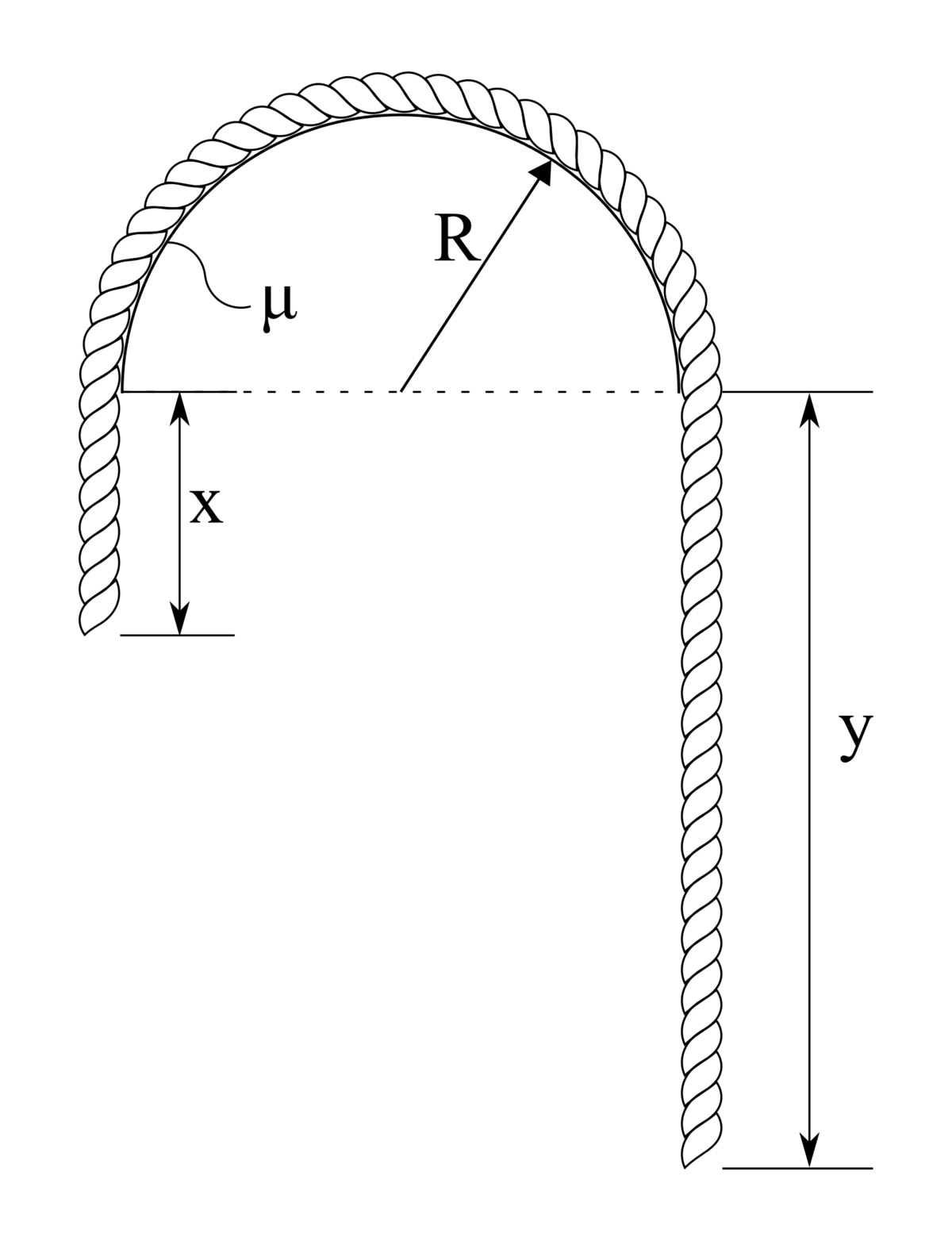
A thin, inextensible rope is placed on a cylinder as in the figure above. The radius is . The friction coefficient between the rope and surface is . The total length of the rope is . What is the maximum ratio so the rope won't start to slip?
Give your answer to 2 decimal places.
Hints :
After writing the equilibrium equations make the following assumptions:
-
.
-
.
You will also encounter a term of the form which you have to neglect.
There is gravity, but the mass of the rope and the gravitational acceleration will eventually simplify.
The answer is 17.03.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's consider a very small element of the rope. We will draw the forces acting on it like in the following picture.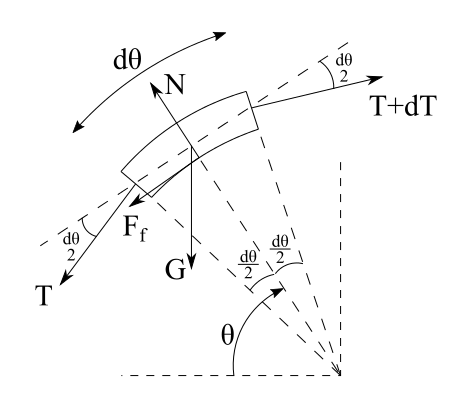
The weight of the element can be written as G = g d m = g λ R d θ . The linear density of the rope λ measured in m k g . Now we write the equations of equilibrium. { N = g λ R d θ sin θ + T sin 2 d θ + ( T + d T ) sin 2 d θ ( T + d T ) cos 2 d θ = T cos 2 d θ + g R λ d θ cos θ + μ N Now we make the assumption that d θ is very small: cos 2 d θ ≈ 1 , s i n 2 d θ ≈ 2 d θ . Also we will ignore the d θ d T term in the first equation. { N = g λ R d θ sin θ + T d θ d T = g R λ d θ cos θ + μ N Be careful that θ is not small and cannot be simplified. After substituting the normal force and making some calculations we get: d θ d T − μ T = g R λ cos θ + μ g R λ sin θ This is a first-order nonhomogeneous linear ordinary differential equation with the tension force as a function of angle: T ( θ ) . At the initial condition the tension is equal to the weight of the x free rope: T ( 0 ) = g λ x Solving the the equation we get the tension in the rope as a function of angle and the lenght of the free part x : T = μ 2 + 1 g λ ( e μ θ ( μ 2 x + 2 μ R + x ) − ( μ 2 − 1 ) R sin θ − 2 μ R cos θ ) Now we can write the tension at the angle π which is equal to the weight of the free part of length y . T ( π , x ) = μ 2 + 1 λ g [ e π μ ( x μ 2 + 2 R μ + x ) + 2 R μ ] We don't forget that the total lenght of the rope is L . We can write 2 conditions: { μ 2 + 1 λ g [ e π μ ( x μ 2 + 2 R μ + x ) + 2 R μ ] = g λ y x + y + π R = L This is a linear system of 2 equations with 2 unknowns. Solving it we finally get: x y = μ 2 + 1 e μ π + μ 2 e μ π − π R − L μ 2 − L + 2 R μ + π R μ 2 + 2 R μ e μ π 2 R μ + 4 R μ e μ π + 2 R μ e 2 μ π After solving it numerically: x y = 1 7 . 0 3 1 7 5