Rotate the ellipse to meet the parabola
The ellipse
is shifted to the right such that its left focus becomes at the origin. Then, the ellipse is rotated, about the origin, counter clockwise by an angle so that it becomes tangent to the parabola . Find the angle of rotation in degrees (choose the smaller of two possible angles), and submit .
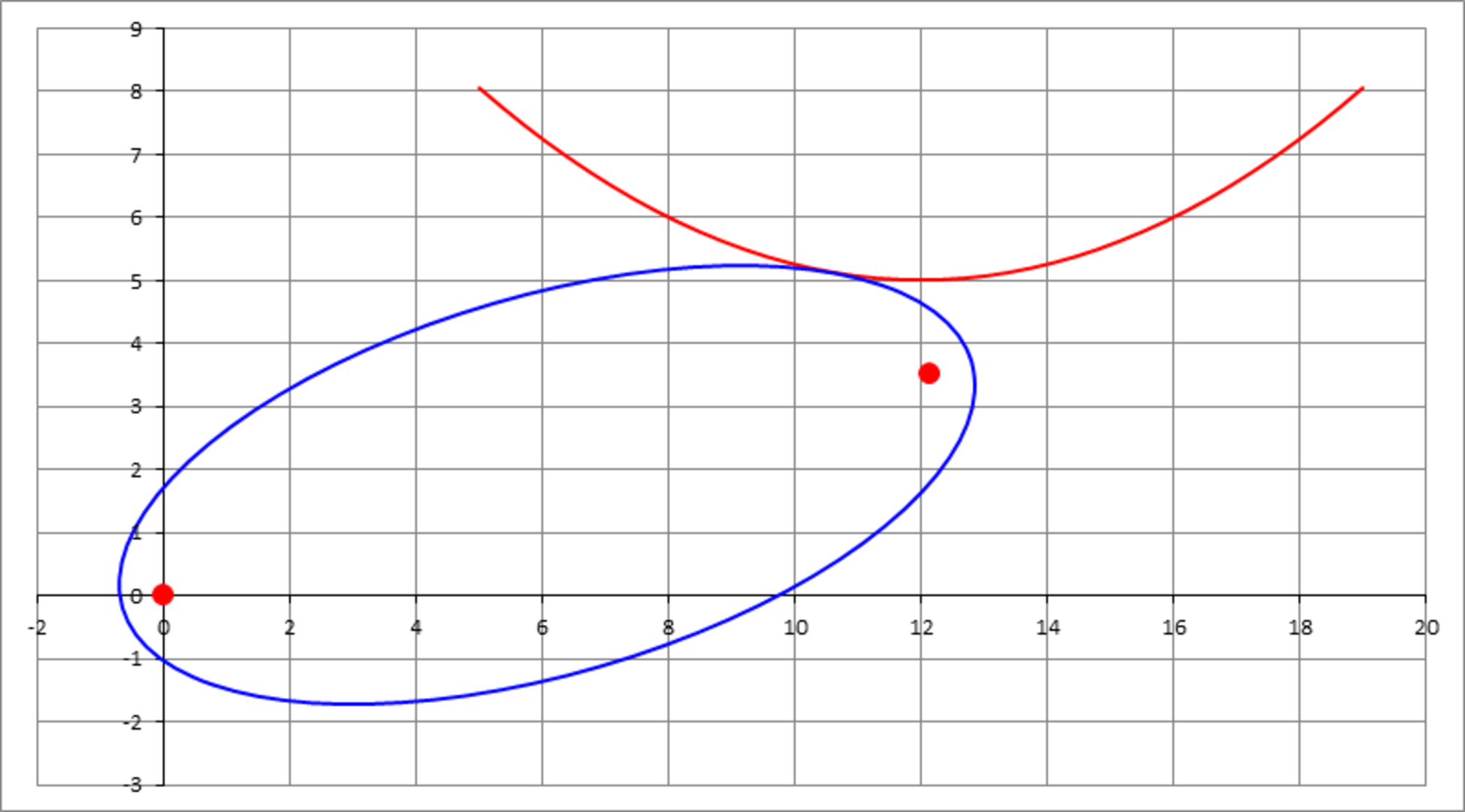
The answer is 1616.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!