Rotate the Vessel
A liquid is kept in a cylindrical vessel, which is being rotated about its axis. The liquid rises at the side, as shown in the diagram.
If the radius of the vessel is 0 . 0 5 m and the speed of rotation is 2 revolutions per second, find the difference in the heights of the liquid at the center of the vessel and its sides (in centimeters).
Take g = π 2 m/s 2 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Why is mgy-1/2 m v^2 constant?
In the first equation, why is it a minus sign? In Bernoulli's Equation it's plus?
Log in to reply
Bernoulli's equation is about fluid particles along the same streamline. It does not apply here.
Log in to reply
I see. What formula are you using then?
View the situation from a rotating frame of reference. The relevant forces are the gravitational force and the centrifugal force (yes, centrifugal -- since we are not working in an inertial frame, this force exists!) Both forces are conservative. The corresponding potentials are U g = m g y and, since F c f = m ω 2 r , U c f = − ∫ 0 r m ω 2 r d r = − 2 1 m ω 2 r 2 , which translates into U c f = − 2 1 m v 2 from a non-rotating point of view.
Since in the rotating frame the fluid is at rest, particles do not experience a net force along the surface. Therefore the surface is an equipotential surface: U g + U c f = m g y − 2 1 m v 2 = const.
here is my solution to this question:-
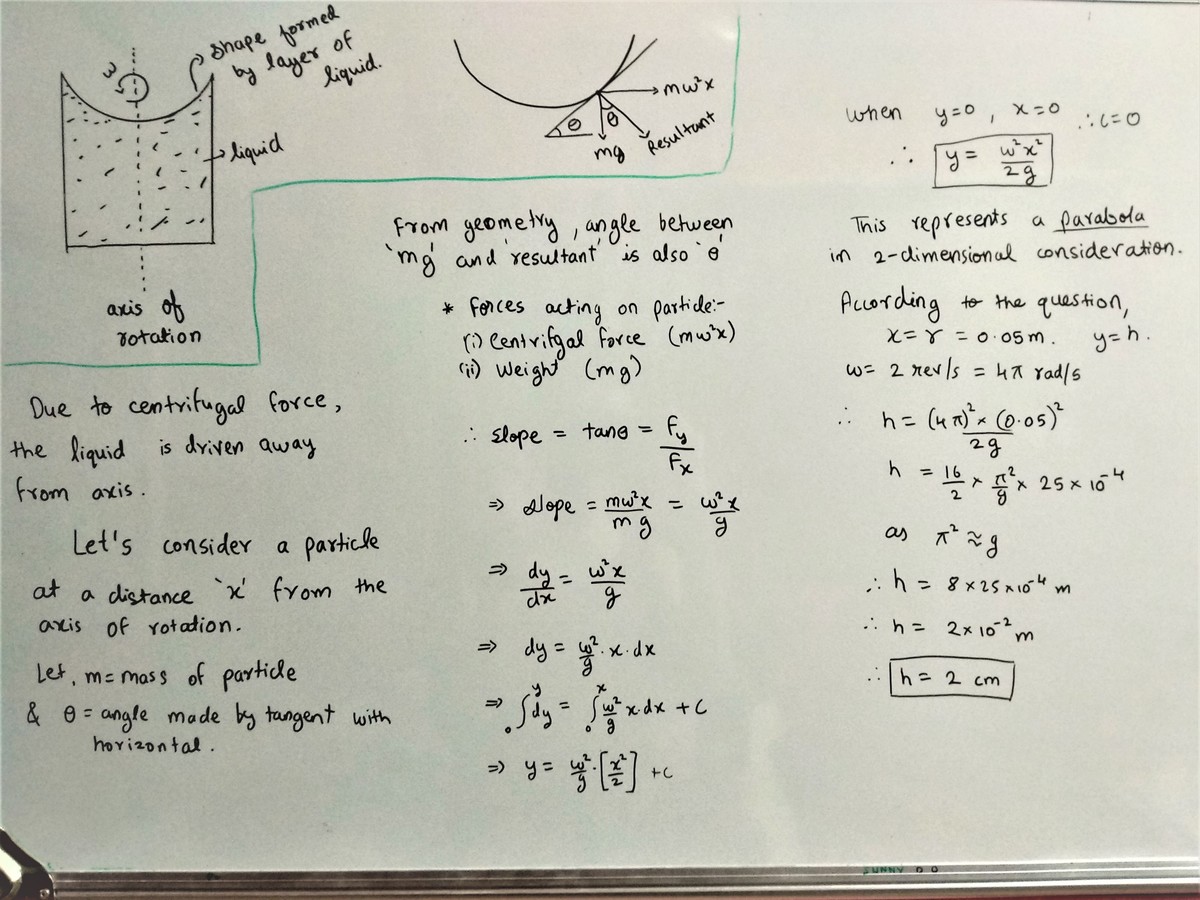
I think centrifugal force doesn't exist? Can it be explained with centripetal force?
Log in to reply
A centrifugal force does exist when you are in a rotating non-inertial frame of reference. It can certainly be explained using centripetal force assuming to be in an inertial frame of reference, after all we are only changing the frame of reference.
You can have a look at my solution in this problem . I have explained it using centripetal force, but the math is essentially the same as taking the centrifugal force.
Log in to reply
Centrifugal force is a pseudo force. It is taken to make the frame of reference inertial, if the system under observation is rotating.
I really love your solution.
Excellent explanation!
Lamba gaya energy conversation se hi ho jata hai and you get your ans due concept of parabola not by the physics
Consider the rotating frame. Acting on a particle of liquid in this frame we have two forces:
- gravity (potential U g = m g h )
- the centrifugal force F = − m ω 2 r , where ω is the angular speed and r is the radius of rotation
The centrifugal force has an effective potential of U c = ∫ F d r = − m ω 2 2 r 2
The surface is an equipotential curve, so it can be described by the equation:
U g + U c = c o n s t .
m g h − m ω 2 2 r 2 = c o n s t .
h = 2 g ω 2 r 2 + c o n s t .
The angular speed is ω = 2 × 2 π = 4 π r a d / s
Therefore the height difference between the centre and the edge is: Δ h = 2 π 2 ( 4 π ) 2 0 . 0 5 2 − 2 π 2 ( 4 π ) 2 0 2 = 0 . 0 2 m
Bernoulli's Equation . d=density of liquid , Then 1 / 2 ∗ d v 2 = d g h where, v = angular velocity * radius solve to get 'h'.
Nah its doesn't work, see my comment on Arjen's solution.
The surface of the liquid will be perpendicular to the total acceleration. (If it weren't, it would flow until it was.)
Therefore the slope of the liquid at any given point is
f ′ ( r ) = g r ω 2 where ω = 2 π f is the angular frequency.
Integrating the slope to get the curve,
f ( r ) = 2 g ( r ω ) 2
Substituting,
f ( 0 . 0 5 ) = 2 π 2 ( . 0 5 ∗ 2 ∗ 2 π ) 2 = 0 . 0 2 , or 2 cm.
Wow. This exact problem (2rps & .05m) is online, only instead of just saying g=π^2, it sets g=10 & π^2=10 (which accomplishes the same thing).
http://physics.qandaexchange.com/?qa=1565/rotating-cylindrical-vessel-with-liquid
Let f ( x ) be the height at radius x with f ( 0 ) = 0 . Water surface will always be orthogonal to total acceleration:
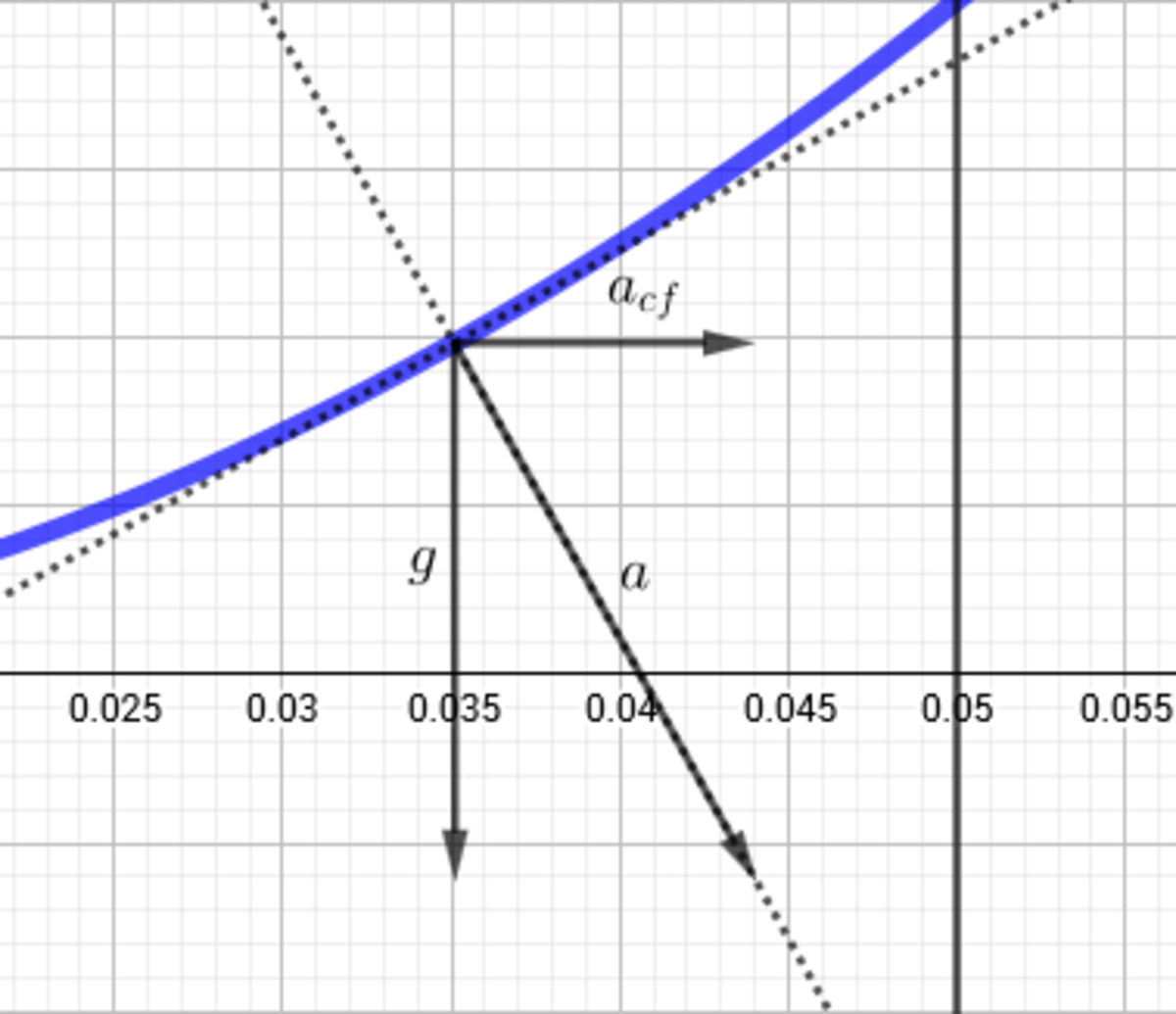
Describing the graph of f as curve ( x , f ( x ) ) with velocity vector ( 1 , f ′ ( x ) ) , and given that centrifugal acceleration at radius x is a c f = ω 2 x , we get that ⟨ ( 1 , f ′ ( x ) ) , ( ω 2 x , − g ) ⟩ = 0 which gives us differential equation f ′ ( x ) = g ω 2 x and with inital condition f ( 0 ) = 0 this gives us f ( x ) = 2 g ω 2 x 2 .
Finally, ω = 2 π f = 4 π r a d / s , and f ( x ) = 8 x 2 . This gives us f ( 0 . 0 5 ) = 0 . 0 2 , i.e. Δ h = 2 c m .
For a particle of mass m at the surface, m g y − 2 1 m v 2 = const. . Thus, comparing a particle at the edge and one in the center, m g Δ h − 2 1 m ( 2 π f r ) 2 = 0 . This simplifies to Δ h = g 2 π 2 f 2 r 2 ; in the given units, π 2 and g cancel, and we have Δ h = 2 ⋅ 2 2 ⋅ ( 0 . 0 5 ) 2 = 0 . 0 2 m = 2 c m .