Rotate to meet the line
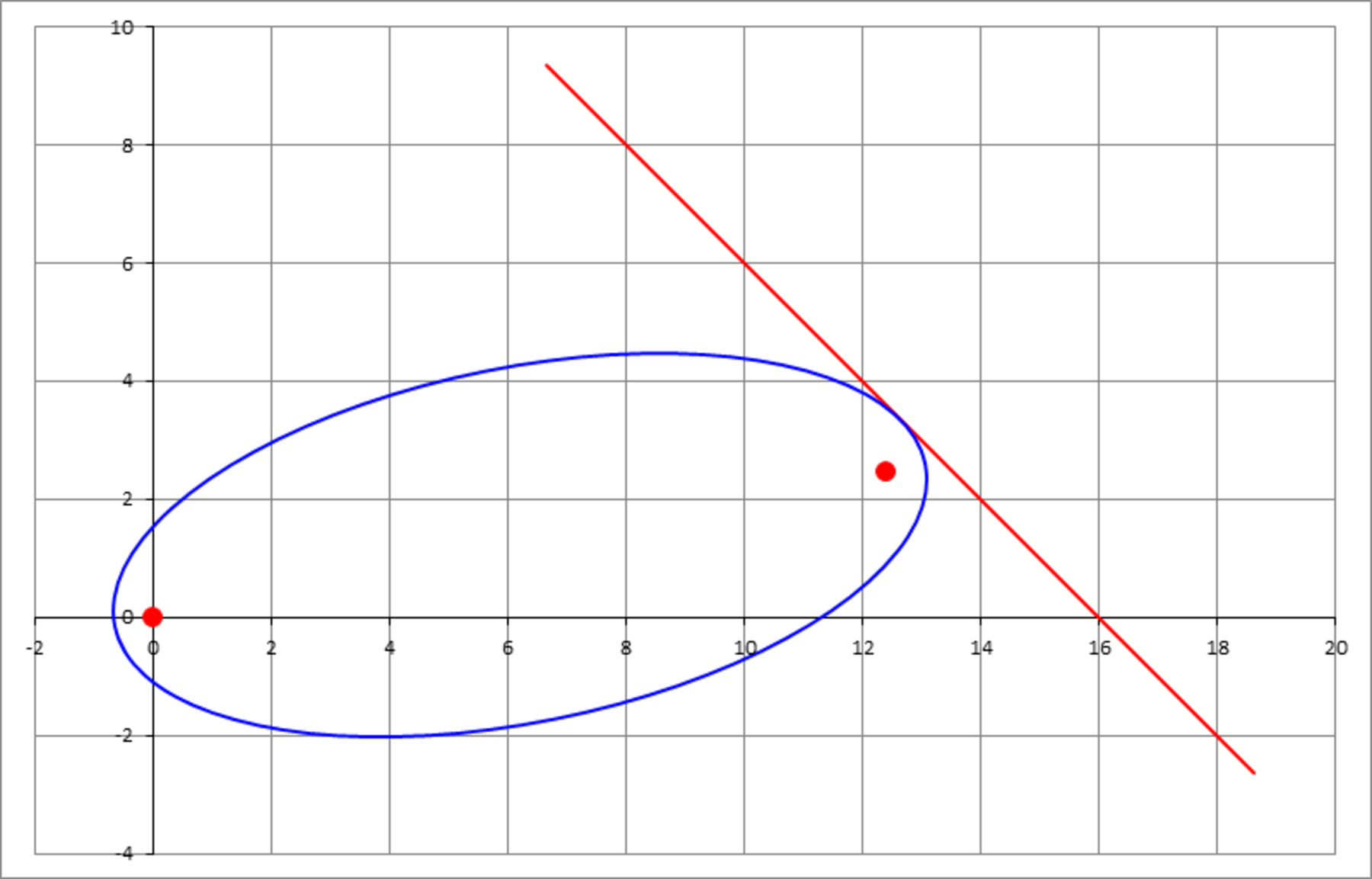
The ellipse
is shifted to the right such that it left focus becomes at the origin. Then, the ellipse is rotated, about the origin, counter clockwise by a certain angle so that it becomes tangent to the line .
Find the necessary angle in degrees that achieves this (choose the smaller of two possible angles), and enter as your answer.
The answer is 1125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The x -coordinate of the left focus is − 7 2 − 3 2 = − 2 1 0 , so the equation of the translated ellipse is 7 2 ( x − 2 1 0 ) 2 + 3 2 y 2 = 1
Now, instead of rotating the ellipse anticlockwise, let's rotate the line clockwise about the origin through the angle θ . To do this, we use the map x ↦ x cos ( θ ) − y sin ( θ ) ; y ↦ x sin ( θ ) + y cos ( θ )
so the equation of the rotated line is x sin ( θ ) + y cos ( θ ) = 1 6 − x cos ( θ ) + y sin ( θ )
which rearranges to y = sin ( θ ) − cos ( θ ) x ( cos ( θ ) + sin ( θ ) ) − 1 6
To find the intersection of the line and the ellipse, we substitute this expression for y into the equation of the ellipse: 7 2 ( x − 2 1 0 ) 2 + 3 2 [ sin ( θ ) − cos ( θ ) x ( cos ( θ ) + sin ( θ ) ) − 1 6 ] 2 = 1
Although this looks pretty hideous, it's just a quadratic in x . Since we want the line to be tangent to the ellipse, we want this quadratic to have exactly one root, so its discriminant must be zero. After some manipulation, this gives the equation 4 4 1 4 csc 2 ( 4 π − θ ) ( − 1 1 9 + 6 4 5 sin ( 4 π + θ ) ) = 0
Dividing through, − 1 1 9 + 6 4 5 sin ( 4 π + θ ) sin ( 4 π + θ ) θ = 0 = 6 4 5 1 1 9 = sin − 1 6 4 5 1 1 9 − 4 π
which works out to be around 1 1 . 2 5 7 0 3 ∘ giving the answer 1 1 2 5 .