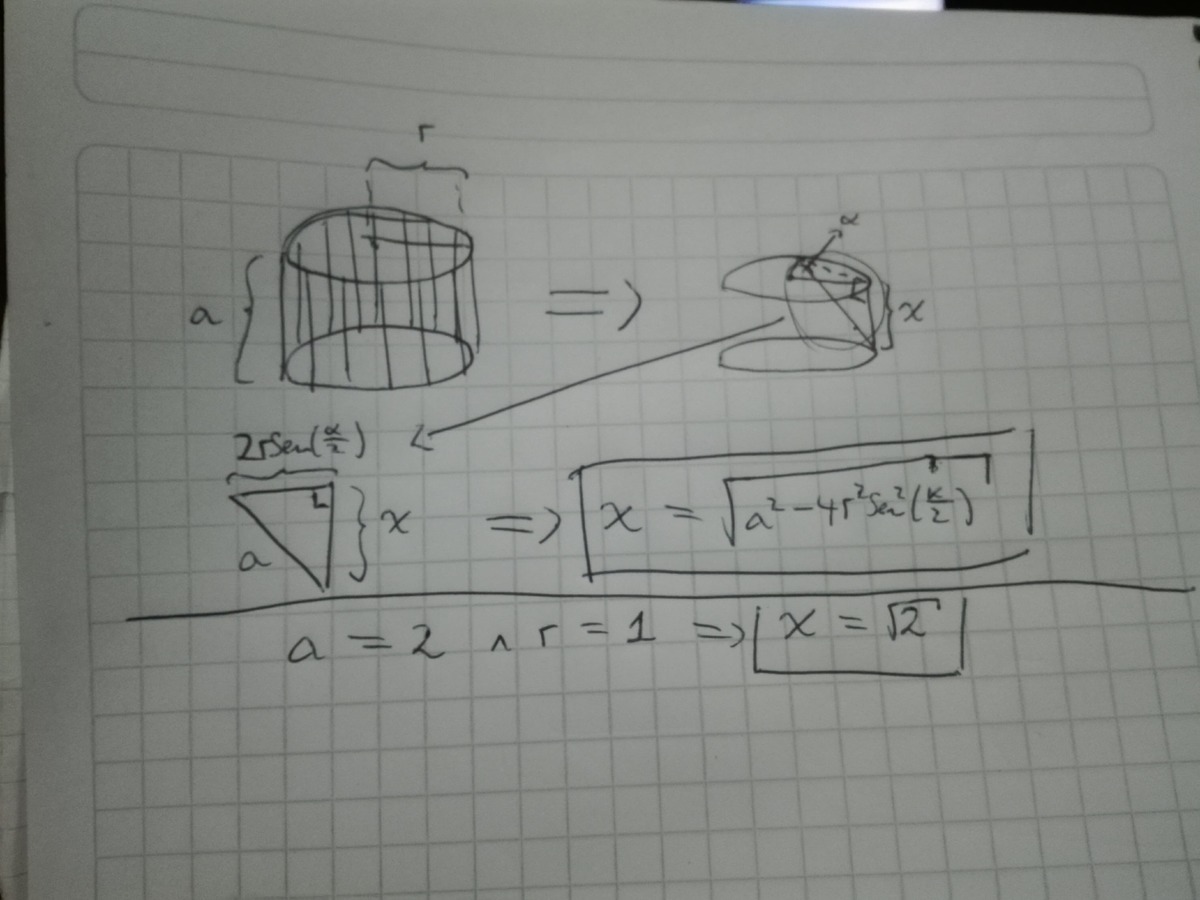
Rotated strings height
Two unit circles are joined by many equally spaced strings of length 2 to form a cylinder. The upper circle is rotated by 9 0 ∘ while the lower is fixed. Naturally, the two circles come closer together.
What is the new distance between them?
The answer is 1.41421356237.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
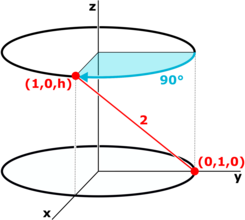 Notice from the figure that the distance between the two shown points is:
2
=
1
2
+
1
2
+
h
2
Hence
h
=
2
≈
1
.
4
1
4
2
Notice from the figure that the distance between the two shown points is:
2
=
1
2
+
1
2
+
h
2
Hence
h
=
2
≈
1
.
4
1
4
2
why is it root 2? where did that come from?
2 = 1 2 + 1 2 + h 2 2 2 = 2 + h 2 2 = h 2 2 = h
i agree with that
Elegant solution using coordinates.
math is insane. there's always a more elegant solution. i did it the way posted just below this, using the pythagorean theorem in two dimensions twice
Why the answer is not √(4-π^2/4)≈1.238 ?If you cut it, you will get a right-angled triangle with a hypotenuse of 2 and a bottom of π/2(2πr/(90/360)=π/2), so the length of the other side is √(4-π^2/4) that is the diastance between the two circles.
Log in to reply
I'm glad you described your thought process.
Using it, the only way this would work is if the string curves along the perimeter of the circle. (i.e. if you were to look top-down, the string's path would appear to trace along the circle, covering a distance of π/2). This arises because of the angle of π/2 radians as you described. In order for the trig to balance out, (a string of length two, being drawn along a circular arc of π/2), you do end up with ≈1.238
However, the string remains tight as the circle is turned 90 degrees or (π/2 radians) and traces a path of a straight line. No π required (unless you want to find the sine and cosine of π/2 to measure planar displacement, which gives x,y coordinates of (1,0) to (0,1) )
The end point has moved left by one radius (1) and down (or up) one radius. When you do this, it affords the solution, as described above, or below.
Only if there had been an animation showing this magnificent motion.. it would have been beyond enlightening.
* * * They can't be unit circles, because strings are being attached to them. Let's say they are unit hoops. They will be closer than the sqrt(2), because strings are pulling against other strings and interfering with how far apart it can be pulled.
We can solve this problem easily by taking into consideration only one of the string (taking all string at once won't make the difference). Now, what's left to do is to map out the movement of that string.
Let's look at both circles on top view:
- The Red X would be the tip of the string at the lower circle and the Red dot would be the tip of the string at the upper circle.
Before Rotation:
After Rotation:
It would seem to appear then that it moved along the X direction by a distance of √2.
Using the information that the string length was 2 and it moved along X by √2. We can calculate the height.
H 2 = 2 2 - √ 2 2
H 2 = 4 - 2
H = √ 2 = 1 . 4 1 4 2 1 3 5 6 2
I was trying to do the same thing But took the curved distance(arc length) instead of straight line (chord)
Rather we can use coordinates to map out.
To solve this problem, I guessed and checked. How does this work? I would rate this problem a 10 because it's confusing.
Can u pls explain how it moved by a distance of √2 and which side is the x-axis
Log in to reply
The red point was moved from the south pole of the circle to the west pole of the circle, so to speak. There is a right triangle formed by the center of the circle, the old position, and the new position. It's a unit circle so each leg is distance 1. Thus the hypotenuse is length sqrt(2).
The string length remains 2.
The horizontal distance between its ends being on a unit circle 9 0 ∘ apart will be 2 .
So the vertical distance between the loops will be 2 2 − ( 2 ) 2 = 2 ≈ 1 . 4 1 4
We can define the lower unit circle to be c 1 and the upper unit circle to be c 2 . Because they are both unit circles where c 2 is rotated over 90 degrees (which equals 2 π rad.) we can say that for a point P on c 1 at time t the coordinates of P would be ( x , y , z ) = ( c o s ( t ) , s i n ( t ) , 0 ) and that for a point Q on c 2 at time t (same variable) the coordinates of Q would be ( x , y , z ) = ( c o s ( t + 2 π ) , s i n ( t + 2 π ) , h ) where h is a constant (between 0 and 2). Our objective is to find the value for h . We know that ∣ P Q ∣ = 2 . This means that ( x P − x Q ) ² + ( y P − y Q ) ² + ( z P − z Q ) ² = 2 ² = 4 and thus that ( c o s ( t ) − c o s ( t + 2 π ) ) ² + ( s i n ( t ) − s i n ( t + 2 π ) ) ² + h ² = 4 . Writing the squares out with some terms switching places gives us ( s i n ² ( t ) + c o s ² ( t ) ) + ( s i n ² ( t + 2 π ) + c o s ² ( t + 2 π ) ) − 2 ( c o s ( t ) c o s ( t + 2 π ) + s i n ( t ) s i n ( t + 2 π ) ) + h ² = 4 . Furthermore, the term c o s ( t ) c o s ( t + 2 π ) + s i n ( t ) s i n ( t + 2 π ) equals c o s ( t − ( t + 2 π ) ) = c o s ( − 2 π ) = 0 because c o s ( u ) c o s ( v ) + s i n ( u ) s i n ( v ) = c o s ( u − v ) . So we get 1 + 1 − 2 ⋅ 0 + h ² = 4 , h ² = 2 and this gives us the final answer: h = 2 = 1 . 4 1 4 . . . The method I used was more complicated than others I have seen for this problem, nevertheless I wanted to share my strategy for solving it.
I also made a figure of what I mean by all this in the picture below (not on scale (some lines are not correct)). The coordinates of point P and Q vary on the circles where they are at (component t involved).
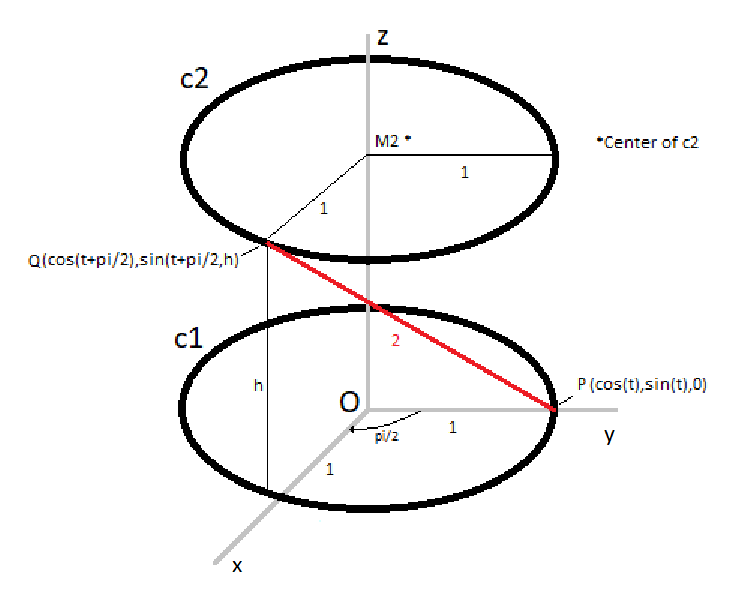
this is exactly what i thought in the first go, but then i thought there has to be a simpler way so i solved like others only. thanks for putting this up here, another method is always appreciated
Could you explain further with some drawings , thanks so much
The top view makes it clear that there are three mutually perpendicular directions with lengths 1, 1 and distance, d. The space diagonal is 2 because it is the unchanging string length.
The 3-d Pythagorean theorem for this is 1 2 + 1 2 + d 2 = 2 2 and solving gives d = 2 ≈ 1 . 4 1 4 2 1 3 5 6
When looking from the top onto the cylinder the original point of each string and the new point create a right angled triangle.
Using Pythagoras the length of the long site can be calculated to be √(2).
When looking from the site onto the cylinder the strings form a right angled triangle again.
The length of the strings (2) is the longest site, while the √(2) calculated above is the base of the triangle. The height of the cylinder is the third site of the triangle.
Using Pythagoras again we can calculate, that
h² = 2² - (√(2))² Root and square cancel each other. h² = 4 - 2 h² = 2 h = √2
primer sansano que veo por aquí 👍
I just kinda got lucky, I realized it was between 0 and 2 but i thought it was exponential and I answered 1.41 or sqrt(2)
Multiply b·h·L where b is the base (b=2), h is the height of the inicial cylinder (h=2) and L is the length of the string (L=2). The outcome of bhL is 8 and that will be a fixed constant. If the string was flexible, by turning the cylinder 90 degrees we would get a new string length of L'=2√2. The height h' would be lower than h and the base b would remain the same. Knowing that b·h·L= 8, b·h'·L' is also equal to 8. Therefore you calculate what the new height h' should be: h'=8/(b·L') or h'=8/(2·2√2)=√2