Rotated strings volume
Two unit circles are joined by many equally spaced strings of length 2 to form a cylinder.
The upper circle is rotated by 9 0 degrees while the lower is fixed. If there were infinitely many strings, they would serve as the surface of a 3D figure, together with the two circles.
What is the volume inside this 3D figure?
The answer is 2.96192195877.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Exactly how I did it. Love the animation, definitely the best answer if you ask me.
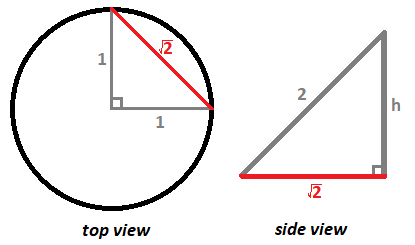
Consider a top view and side view of one of the strings. From the top, the string appears to have a length of 1 2 + 1 2 = 2 (as a hypotenuse of a right isosceles triangle with unit legs). From the side, the height of the 3D figure would be the leg of the right triangle that has a hypotenuse of the actual string length of 2 and a leg of the apparent top view string length of 2 , which would be h = 2 2 − ( 2 ) 2 = 2 , making another right isosceles triangle.
Let x be the vertical distance away from the center of the 3D figure. Then another right triangle is formed in the top view with x and 2 2 as legs and the radius r of each horizontal circle cross-section as a hypotenuse, and so r 2 = x 2 + ( 2 2 ) 2 = x 2 + 2 1 .
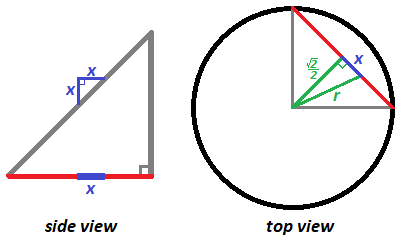
The volume of the upper half of the 3D figure is then V = π ∫ 0 2 2 x 2 + 2 1 d x = 3 π 2 , and since the 3D figure is symmetrical, both halves would have a volume of V = 2 ⋅ 3 π 2 ≈ 2 . 9 6 1 9 2 1 9 5 8 7 7 .
This solution is inaccurate. The geometry finding the radius of the smallest inner circle is correct, but the integral is flawed. You took an integral of an expression for r^2 but then integrated with respect to x without doing a substitution that respected the chain rule. Where this conceptually causes a disconnect is that the radius of the circles being stacked together does not change at a linear rate. The integral assumes x changes linearly, but in fact it follows a sinusoidal function. When I solved this, I created a sin function to model the curve created by the strings and then rotated about the center of the circle. The function came out being -(1- sqrt(2)/2) (sin( pi*x/sqrt(2)) + 1. This rotation comes out at about 2.9766.
Log in to reply
On a vertical cut of the figure passing through the axis of rotation, the curve generated by the strings is actually a hyperbola, you could fit one using some known points and then integrate as a rotation solid, the result you obtain is exactly the same that David got 3 2 π 2
As Jose said, the curve is a hyperbola. If you agree with my solution for finding the radius, then you see that r 2 = x 2 + 2 1 , which can be rearranged to 2 r 2 − 2 x 2 = 1 , an equation of a hyperbola. In my solution, x = 0 is the center of the 3D object, but in your sine function it looks like x = 0 is the bottom of the 3D object, so we can adjust my hyperbolic equation to match your function by replacing x with x − 2 2 , and so 2 r 2 − 2 ( x − 2 2 ) 2 = 1 which makes the r function r = ( x − 2 2 ) 2 + 2 1 . I'll bet if you used this function instead of your sine function you would come up with the same answer as me.
As far as the integration goes, I used horizontal cross-sections that were circles, and so V = ∫ π r 2 . There should be no need to do a substitution with respect to the chain rule.
Log in to reply
Agreed, I thought about that integral as well for this problem. V = ∫ π r 2
My solution is identical to David Vreken's but I thought this problem was fun so I made a Desmos graph to show the hyperbola.
The dotted circle is the top view with two points that are 90 degrees apart going around it.
The purple horizontal lines transfer the y-coordinates to the side views of the circles (that appear as black line segments.) Each purple intersects the opposite side.
Connecting these points of intersection is the blue line representing the strings.
I also added the hyperbola in blue so you can see it being traced out. You can also click #13 to toggle the shape of interest.
Desmos needs a way to have thicker and thinner lines and a wider color palette.
That "Here it is" hotlink gave me the awesome chills. Absolutely Beautiful visualization. Thanks.
Had it not been the last problem of the advanced section I would have done it much Earlier; Anyways Here's what I have done. Part 1 Consider the bottom circle to be the reference and let h be the height you rise from the bottom plane; From here onwards assuming that you know the distance between the two planes is 2 ; Now, why does the cylinder squeeze before all? It is because when you consider a point P ( x 0 , y 0 ) on the rim of the bottom circle (say C 0 ) it is mapped to some point Q ( x 1 , y 1 ) on the top circle say C 1 by some transformations which can be as purely as translational as T : { x = x 0 ± λ y = y 0 ∓ λ and; Now we see that by rotating the top circle by 2 π we applied the transformation T on all points ( x , y ) on the line PQ. I hope this suffices to elucidate why the cylinder squeezes on torsion. Part 2 Let y be the distance a point X ( x , y ) travels radially while moving a distance h up the cylinder; Now proportionally, we can say that y = h . 2 because when h = 2 , y = 2 . Now let A be the area of the disc with r = ( 1 − y ) as radius. So A = π . ( 1 − h . 2 ) 2 .Consider an elemental height d h at a distance h from the base of the cylinder. The volume of this element is d v = π . ( 1 − h . 2 ) 2 . d h . Integrating this element from 0 to 2 2 and letting the total volume to be V we get 2 V = π . 3 2
this gives V = 2 π 3 2 = 2 . 9 6 1 9 2 1 9 5 8 7 7 and the Last problem of Advanced section is down
Let's look at both circles on top view:
- The Red X would be the tip of the string at the lower circle and the Red dot would be the tip of the string at the upper circle.
Before Rotation:
After Rotation:
It would seem to appear then that it moved along the X direction by a distance of √2.
Using the information that the string length was 2 and it moved along X by √2. We can calculate the height.
Side View:
H 2 = 2 2 - √ 2 2
H 2 = 4 - 2
H = √2
As the top circle rotates to 90 degress, a smaller circle begins to emerge at the middle of the whole object.
Since the whole object was a prismatoid, we can use the Prismoidal Formula : V = 6 H ( A 1 + A m + A 2 )
V = 6 √ 2 ( π + 4 ( 0 . 5 π ) + π )
V = 3 2 √ 2 π = 2 . 9 6 1 9 2 1 9 5 8 7 7
Setting the bottom circle on the xy plane with its centre at the origin, the z axis going through centre of the volume through the top circle's centre. We know the hieght is 2 from a previous basic question. The volume is V=\pi\int_0^\sqrt2{x^2+y^2}dz where x , y and z follow one of the lines and we're simply integrating the area of the circles times d z from bottom to top. One of the lines passes from ( 1 , 0 , 0 ) to ( 0 , 1 , 2 ) . Its parametric equation is ( 1 − t , t , 2 t ) . Substituting t into V yields: V = π ∫ 0 1 ( 1 − t ) 2 + t 2 2 d t = 2 π ∫ 0 1 1 − 2 t + 2 t 2 d t = 2 π ( t − t 2 + 3 2 t 3 ) ∣ 0 1 = 3 2 2 π ≈ 2 . 9 6 1 9 2 1 9 5 8 7 7 2 2 4 4
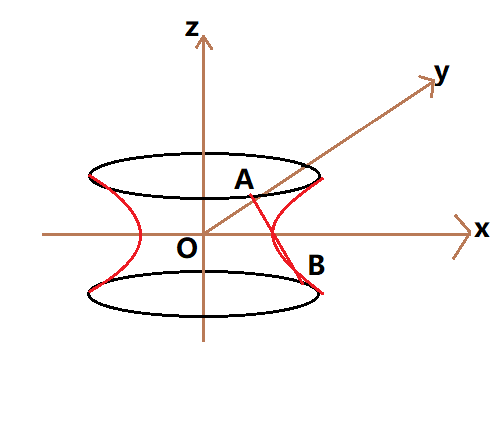
I solve it by using the 3-dimensional coordinate system.
We have x-axis and z-axis on the screen and y-axis toward into the screen. It is easy to see that the distance between two rings be 2 (You can see David's solution), then let an arbitrary red line have intersection A and B on the top ring and the bottom ring respectively.
Then, we can set A ( cos μ , sin μ , 2 1 ) , B ( − sin μ , cos μ , − 2 1 ) by the knowing that − 2 π ≤ μ ≤ 0 . This is because we want to determine the function of the right-side curve in terms of x and z . But we will end up in parameter form, it is easier.
Let a point P be the intersection point of line A B and the plane y = 0 , that is P ( x , 0 , z ) , we have A P < x − cos μ , − sin μ , z − 2 1 > = k A B = k < − sin μ − cos μ , cos μ − sin μ , − 2 > We will get the expression of k : k = sin μ − cos μ sin μ
Substituting these into the expression of x and z get x = cos μ − k ( sin μ + cos μ ) = cos μ − sin μ 1 = 2 cos ( μ + 4 π ) 1 and also z = 2 1 − 2 k = 2 1 tan ( μ + 4 π )
For the sake of simplicity, we use μ + 4 π = θ and change the range to − 4 π ≤ θ ≤ 4 π , we get simpler parameter form of x and z : x = 2 1 sec θ , z = 2 1 tan θ As you can see, this is the parameter form of hyperbola .
Do some integral to get the volume:
∵ z ∴ d z ∴ V = 2 1 tan θ = 2 1 sec 2 θ d θ = ∫ π x 2 d z = 2 2 π ∫ − 4 π 4 π sec 4 θ d θ = 2 2 π ∫ − 4 π 4 π ( 1 + tan 2 θ ) d tan θ = 2 2 π ( tan θ + 3 1 tan 3 θ ) ∣ ∣ ∣ ∣ − 4 π 4 π = 3 2 4 π
I don't know if it was fair, but instead of reinventing the wheel I remembered the formula
V = 3 ( 2 a 2 + r 2 ) h π
where a = 2 1 is the radius at the middle height.
It's easy to remember: if a=0, you get two cones, if a=r you get a cylinder.
It's obvious that each cross section of the figure parallel to bases is a circle. Then, it's evident that we should integrate area of these circles with respect to the height of the figure: V f = ∫ 0 H r ( h ) 2 π d h where r ( h ) is a radius of the circle at the height h . From the corresponding problem in basic section , we know that H = ∣ A B ∣ = 2 , where A B is a chord which joins two, 9 0 degrees apart, points on the base circle. Also, as H and A B form isosceles right triangle, we have h ( x ) = x where x is the distance from B along A B . Observe how moving along H is equivalent to moving along A B . That allow us to rewrite our formula and instead of integrating with respect to h , we integrate with respect to x : V f = ∫ 0 ∣ A B ∣ r ( x ) 2 π d x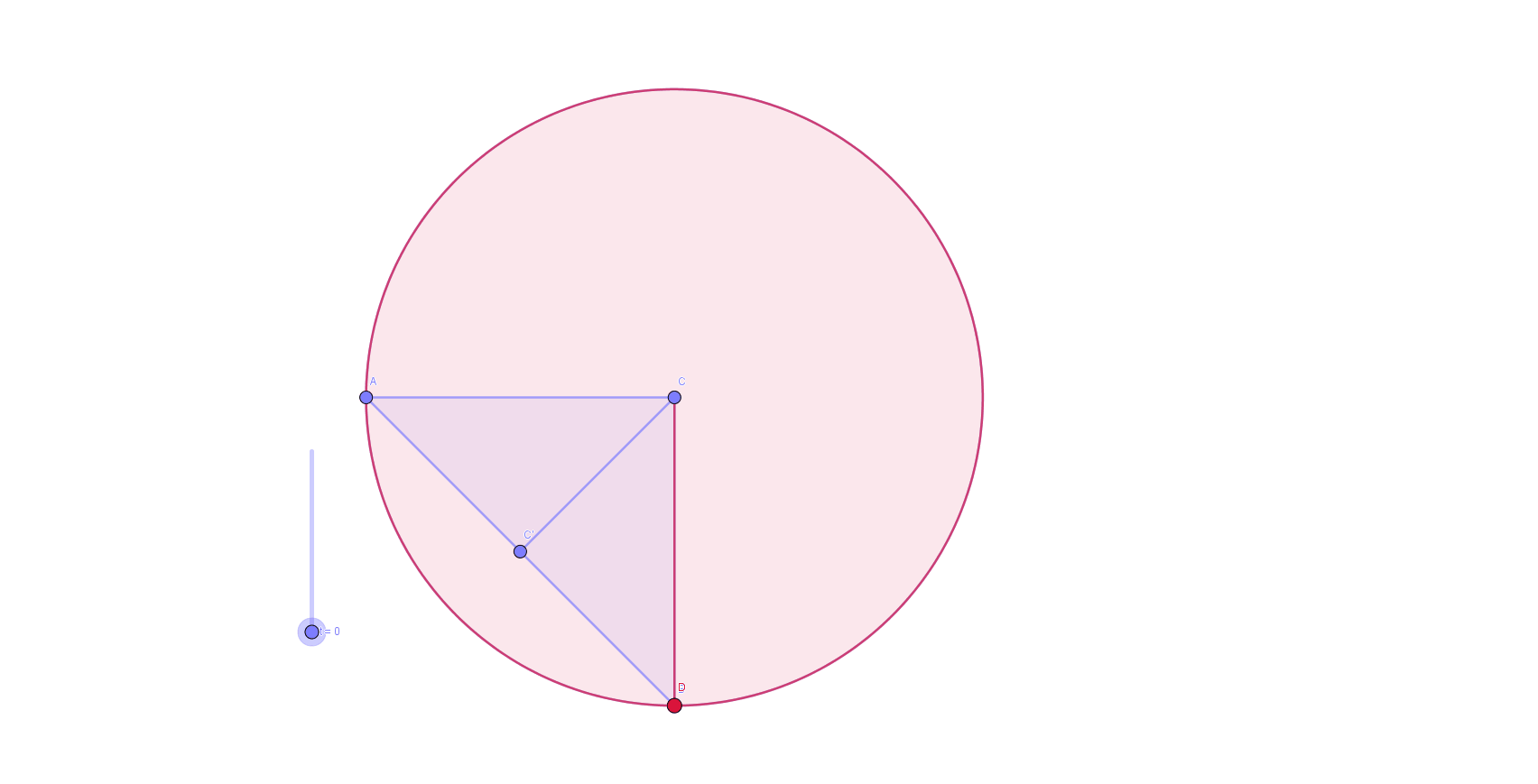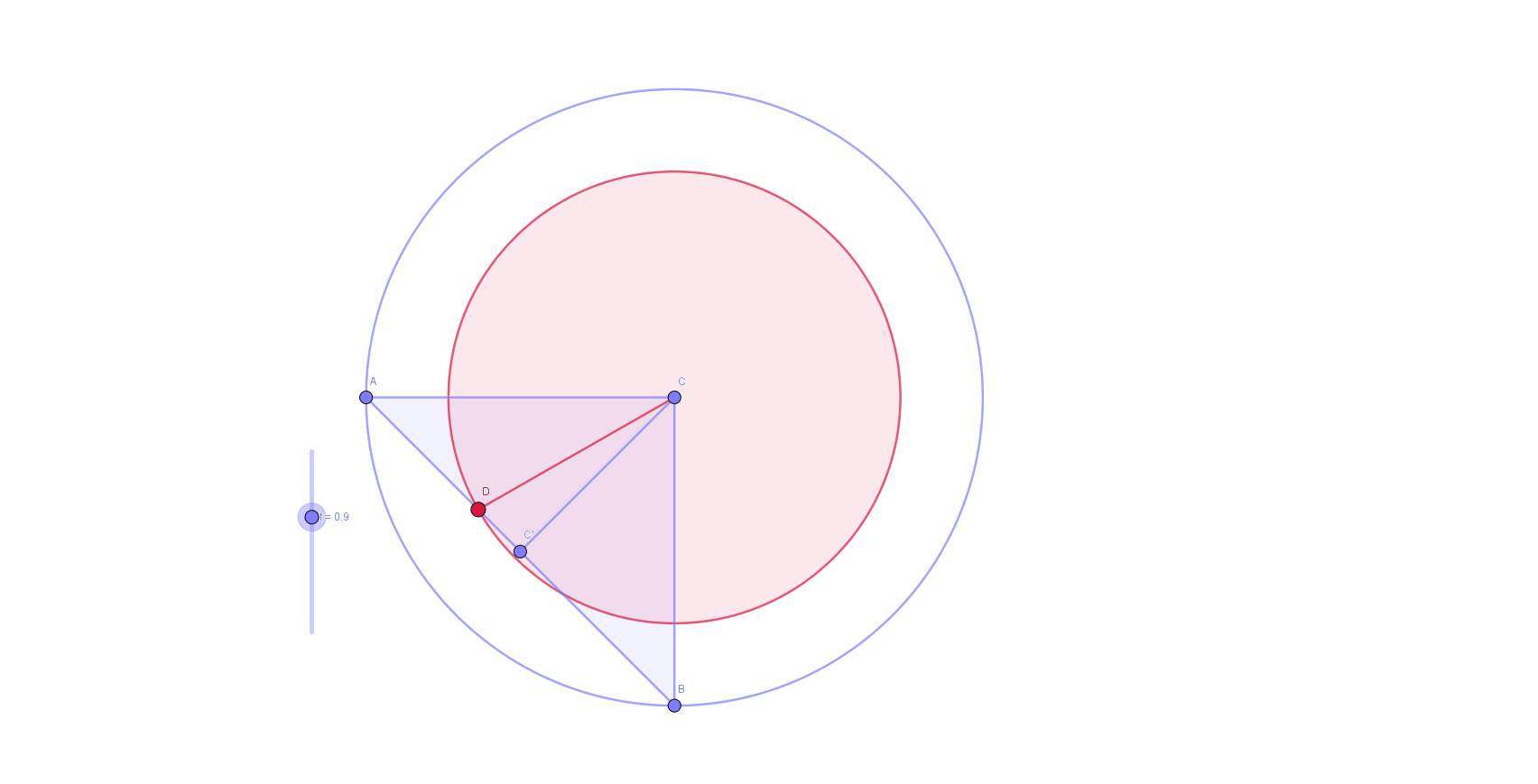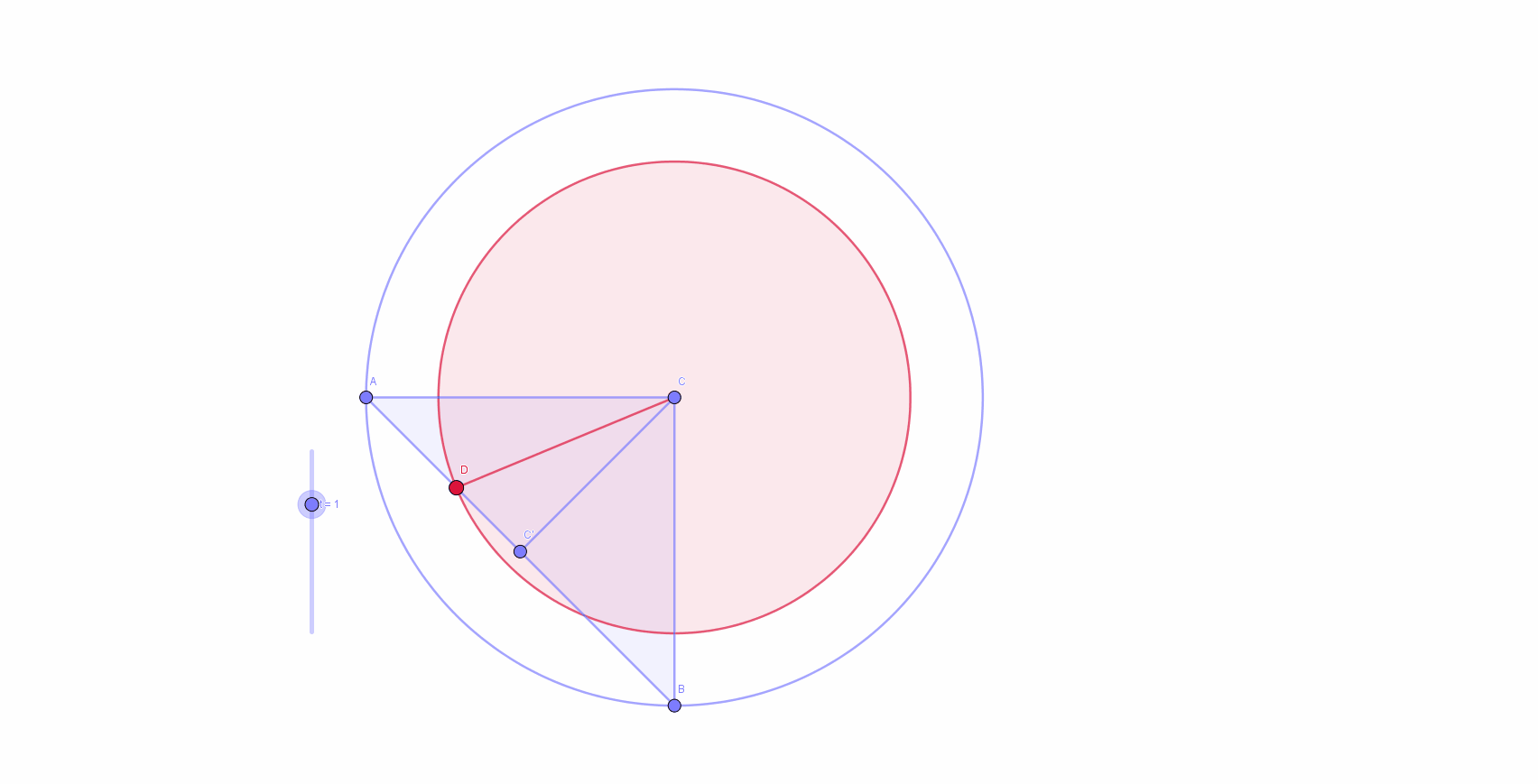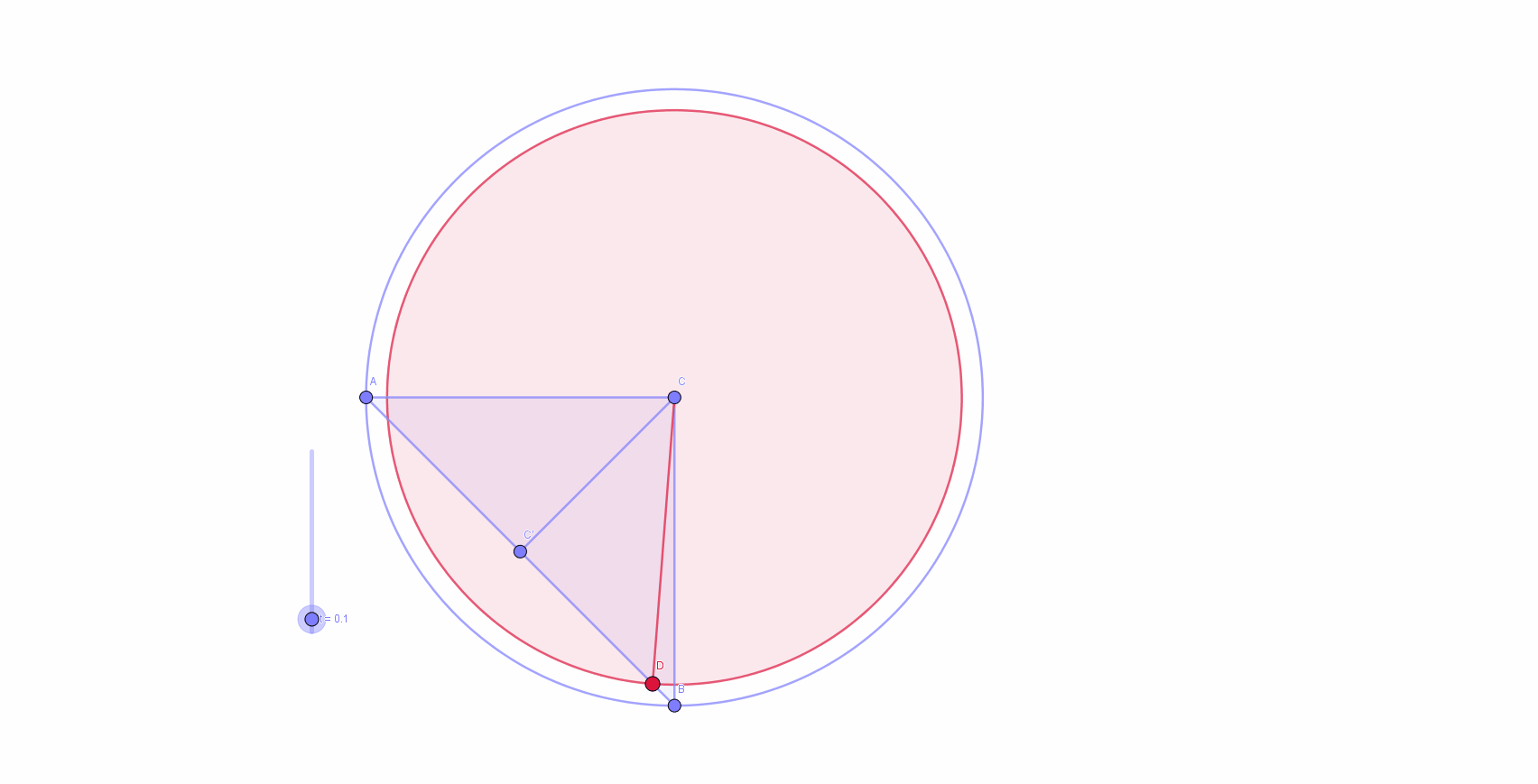 Animation of behavior of
r
with respect to
x
By cosine theorem we have:
r
2
=
x
2
+
1
2
−
2
x
cos
4
5
∘
=
x
2
+
1
−
2
x
2
2
=
x
2
−
2
x
+
1
Animation of behavior of
r
with respect to
x
By cosine theorem we have:
r
2
=
x
2
+
1
2
−
2
x
cos
4
5
∘
=
x
2
+
1
−
2
x
2
2
=
x
2
−
2
x
+
1
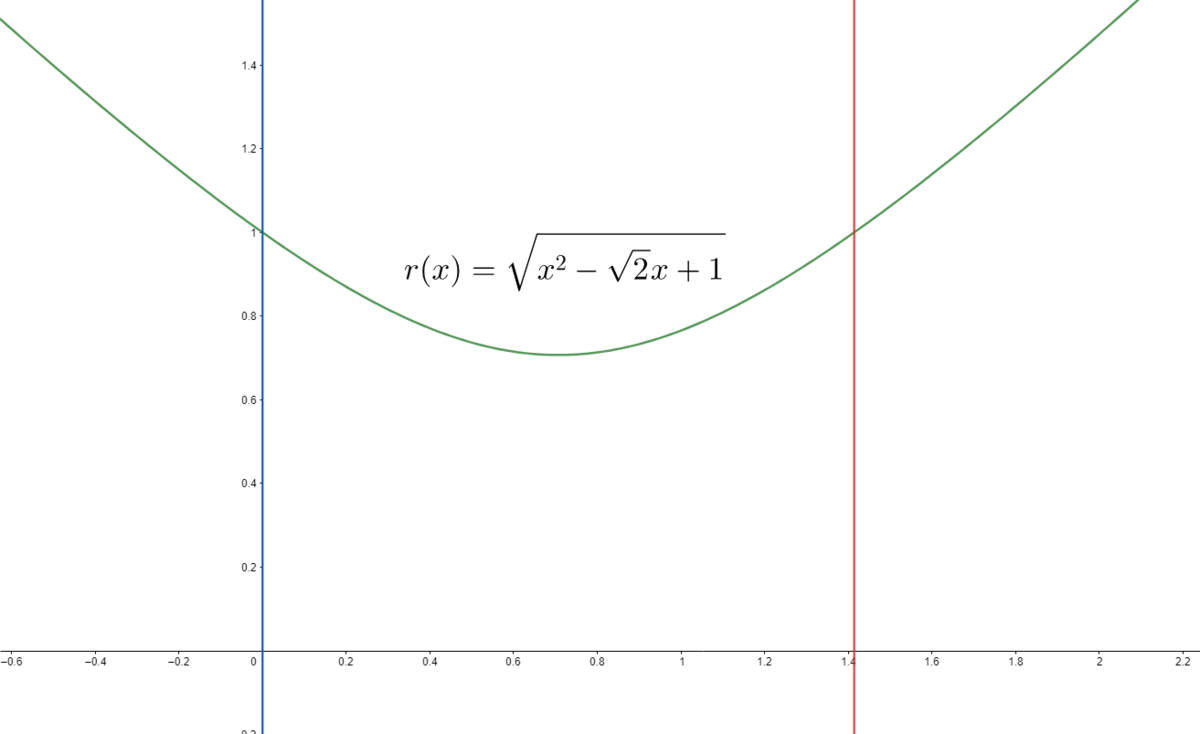 The graph resembles the curvature of the figure at the given image
Now, we integrate:
V
f
=
∫
0
∣
A
B
∣
r
(
x
)
2
π
d
x
=
π
∫
0
2
x
2
−
2
x
+
1
d
x
=
π
∫
0
2
x
2
d
x
−
π
2
∫
0
2
x
d
x
+
π
∫
0
2
1
d
x
=
π
[
3
x
3
]
0
2
−
π
2
[
2
x
2
]
0
2
+
π
[
x
]
0
2
=
3
2
π
2
−
π
2
+
π
2
=
3
2
π
2
≈
2
.
9
6
1
9
2
2
The graph resembles the curvature of the figure at the given image
Now, we integrate:
V
f
=
∫
0
∣
A
B
∣
r
(
x
)
2
π
d
x
=
π
∫
0
2
x
2
−
2
x
+
1
d
x
=
π
∫
0
2
x
2
d
x
−
π
2
∫
0
2
x
d
x
+
π
∫
0
2
1
d
x
=
π
[
3
x
3
]
0
2
−
π
2
[
2
x
2
]
0
2
+
π
[
x
]
0
2
=
3
2
π
2
−
π
2
+
π
2
=
3
2
π
2
≈
2
.
9
6
1
9
2
2