Rotating a Graph?
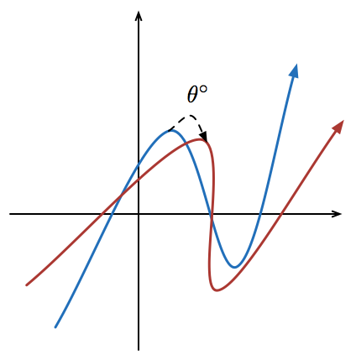 The above shows twos functions on a same Cartesian Plane:
and
colored blue and red respectively.
The above shows twos functions on a same Cartesian Plane:
and
colored blue and red respectively.
Let
Define , where , as the new graph obtained by rotating the graph of degrees about the origin ( ) in the clockwise direction.
Find the maximum value of such that for all values of , has every value of paired with only one (more simply, no two points can have the same -coordinate).
Input your answer as . Where is the floor function which means the greatest integer less than or equal to .
This is part of the set Trevor's Ten
The answer is 946.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We want to find the maximum NEGATIVE slope of the function since to be a non surjective function, there must be at least one point on the graph that has an instantaneous slope of ± ∞ (note that a slope of ∞ is the same as a slope of − ∞ ). Imagine the line tangent to f ( x ) with the most negative slope. We need rotate that till it's perpendicular with the x-axis.
We normally take the first derivative for slope. But here, we need to take the second derivative and set it equal to 0 since we need to find the global minimum of the first derivative. Hence
f ( x ) = x 3 − 6 x 2 + 6 x + 1
f ′ ′ ( x ) = 6 x − 1 2
Setting this equal to 0 to find the minimum of f ′ ( x )
0 = 6 x − 1 2
2 = x
Plugging this into f ′ ( x )
3 x 2 − 1 2 x + 6 = s l o p e
3 ( 2 ) 2 − 1 2 ( 2 ) + 6 = s l o p e
− 6 = s l o p e
If anyone needs an explanation of this next concept, please comment below.
Now, we take the arctan of this measurement to get the angle of this slope WRT to the x-axis ( ar g ( x ) ).
tan − 1 ( ∣ − 6 ∣ ) ≈ 8 0 . 5 3 7
Now, we need a right angle
9 0 = θ m + 8 0 . 5 3 7 7
9 . 4 6 2 = θ m
If we rotate the graph anymore than this clockwise, there will be two points with the same abscissa and different ordinate . Thus we have created a function with two y's per x