Rotating a superconducting loop
A superconducting (zero resistivity) loop of area A = 1 0 − 2 m 2 is placed in a constant magnetic field of induction B = 1 0 m T so that its plane is parallel to the magnetic field. The ring is now rotated so that the magnetic field forms an angle of 3 0 ∘ with its plane. What will be the current in Amps in the loop after it is rotated if its inductance is L = 1 μ H ?
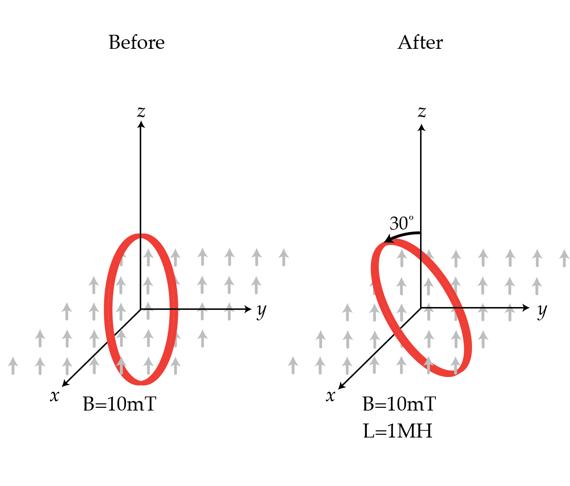
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
We have dϕ = L x dI where ϕ = magnetic flux
and I = current
now initially ϕ = I = 0
finally ϕ = B . A
= BA cosθ where θ = 60
so dϕ = 5 x 10^(-5) Weber
so dI = dϕ/L
= { 5 x 10^(-5)} / {10^(-6)} Amp
= 50 Amp.
which is final current as initial current was zero.
The emf is given by V=d(flux) /dt, and the self inductance is given by V=L dI/dt. Equating the two we get d(flux) =L dI The total change in flux is ABsin30 = 5x10E-5 Tm^2. Hence I=(5x10E-5)/(1E-6) = 50A
Since the loop is superconducting
R
=
0
we have that
E
=
I
R
=
0
.
On other hand, from Faraday's Law we know that
E
=
−
d
t
d
Φ
.
Therefore the magnetic flux through the loop cannot change i.e.
d
t
d
Φ
=
0
. In other words,
Φ
i
=
Φ
f
.
Since initially, the plane of the loop is parallel to magnetic field we have that
Φ
i
=
0
When the loop is rotated, the magnetic flux is
Φ
f
=
L
I
f
+
B
A
cos
(
9
0
∘
−
3
0
∘
)
Setting the final flux equal to the initial flux we obtain
∣
I
f
∣
=
2
1
L
B
A
=
5
0
A
.
Note that the negative sign of the current indicates its direction which can be also determined from Lenz's Law.
By the definition V = L d t d i , where V is the voltage induced across the circuit, L is the inductance (Henries), and d t d i (the time rate of change of current with respect to time), we know how to relate one of the quantities we do know L to current i . However, let's get rid of voltage.
By Faraday's law of induction, we can relate an electromotive force (or voltage) E to the time rate of change of electric flux Φ in the following way E = − d t d Φ .
Because the coil here is a superconductor, there is no resistance. Thus, V = E . And then we can set these two equations equal to each other.
L d t d i = d t d Φ (the negative sign can be eliminated)
Eliminate d t .
L d i = d Φ
Then we can integrate, pulling out our inductance L because it remains constant.
L i = Φ and i = L Φ follows.
Returning to the diagram, we see that initially the flux Φ = B ⋅ A was 0, because there are no field lines passing through the closed loop circuit. Or mathematically, B ⋅ A = 0 , where A is the area vector directed perpendicular to the loop.
In the second case, B ⋅ A = 0 , and actually B ⋅ A = , after a little geometry, 0 . 0 1 × 0 . 0 1 × cos ( 6 0 )
i = L Φ ⇒ 5 0 A