Cube Revolution

Consider rotating a unit cube about the axis passing through two opposing vertices.
What is the volume of the revolution solid?
If the answer can be expressed as b a π , where
- a , b are both positive integers, and
- a is square-free,
input a × b as your answer.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The top and bottom portions are clearly cones. The curved bit in the middle is a bit trickier, but from experience, I know that if you revolve a skew line about an axis a hyperbola is formed.
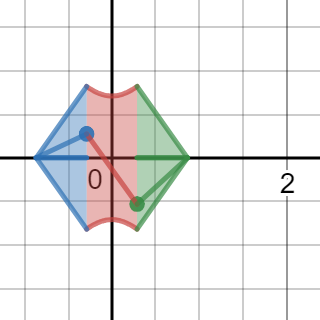
Check this for an animated version https://www.desmos.com/calculator/042ofzxcec
I just need to think about how to get that hyperbola.
The long axis of the cube is 3 and the cones each have height 3 3 so the width of the inner part is also 3 3
When you are viewing the cube so you can just see two faces, you are also seeing the full width of the cone (on one side). This works out to 3 6 .
Not only is this the radius of the cone, it also gives two points on the hyperbola ( ± 6 3 , 3 6 )
The vertex of the hyperbola can be seen when one of the corners is pointing directly at you. It is ( 0 , 2 2
These points are enough to find the equation of the hyperbola. The top half can be written as y = 2 1 + 2 x 2
This is enough to start finding the volumes:
Each cone is 3 1 π ( 3 6 ) 2 6 3 = 2 7 2 π 3
The hyperbola of revolution is π ∫ 6 − 3 6 3 ( 2 1 + 2 x 2 ) d x = 2 7 5 π 3
Add the two cones and the hyperbola of revolution to get the nicely reducing total 3 π 3
So the solution is 3 ∗ 3 = 9
The revolution solid is made up of two cones, one at the top ( V top ) and another at the bottom ( V bottom ) , and a weird shape ( V weird ) in between.
It seems like the volume of the cones can be easily calculated, as the radius of the base side is 3 2 and the height is 3 1 .
V top = V bottom = 3 1 π ⋅ ( 3 2 ) 2 ⋅ 3 1 = 2 7 2 3 ;
∴ V top + V bottom = 2 7 4 3 π .
The sides cannot make the outer area, it's the corners that makes the outer area.
Knowing that and looking at the gif above, and possibly with your head going dizzy, you can see that only one corner rotating 3 6 0 ∘ can make V weird .
Then it is natural to be eager to know the distance between the corner and the axis.
Let there be a unit cube peacefully lying on an x y z coordinates system with one vertex at the origin and three vertices at ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) .
There's a straight line l , stretching from ( 0 , 0 , 0 ) to ( 1 , 1 , 1 ) . Define l = ( 1 , 1 , 1 ) .
Point P ventures from ( 1 , 0 , 0 ) to ( 1 , 0 , 1 ) with constant speed, and point H is the foot of perpendicular from P to l .
Let P ( 1 , 0 , t ) , H ( s , s , s ) .
P H ⋅ l = 0 , and you get t = 3 s − 1 . Knowing that 0 ≤ t ≤ 1 , we see that 3 1 ≤ s ≤ 3 2 , and therefore,
H ventures from A ( 3 1 , 3 1 , 3 1 ) to B ( 3 2 , 3 2 , 3 2 ) with constant speed.
Then let H be defined again as A H = x , where x increases with constant speed. ( H is still on l . )
Note that H moves a distance of 3 1 with constant speed and P moves a distance of 1 with constant speed, and therefore P ( 1 , 0 , 3 x ) .
Then O H = 3 1 + x and O P = 1 + 3 x 2 , and since ∠ P H O = 9 0 ∘ ,
P H 2 = 2 x 2 − 3 2 x + 3 2 .
Note that
V weird = ∫ 0 3 1 ( π ⋅ P H 2 ) d x = π ∫ 0 3 1 ( 2 x 2 − 3 2 x + 3 2 ) d x = π [ 3 2 x 3 − 3 1 x 2 + 3 2 x ] 0 3 1 = 2 7 5 3 π
From above, the final sum we're trying to get, V top + V bottom + V weird = 2 7 9 3 π = 3 3 π .
∴ a × b = 3 × 3 = 9 .