Rotating Cylinder
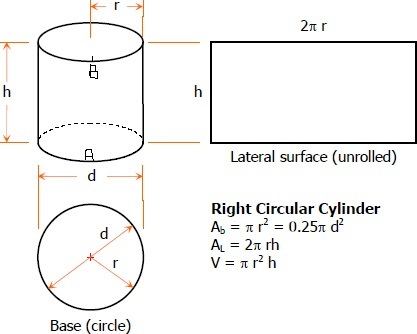A right circular cylinder with base circumference equal to 80 cm, has height equal to 60 cm. It is rotating about its axis at a speed of 30 degrees a second. A boy holds a marker at a point A on the base circumference. He draws a line by taking the marker straight upwards, perpendicular to the base, with a uniform speed of 5 cm per second, and stops at the top at point B. Find the length of the line thus drawn.
DETAILS
give the answer in cm
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
the cylinder takes 12 seconds to rotate, the boy also takes 12 seconds to draw the line so the point B must be above point A such that AB is equal to h. In the cylinder's unrolled form, the line drawn will be equal to the diagonal of the rectangle. So using the Pythagoras theorem
diagonal^2 = circumference^2 + height^2
therefore diagonal is equal to (80^2 + 60^2)^(1/2) = 100