Rotating Fluid
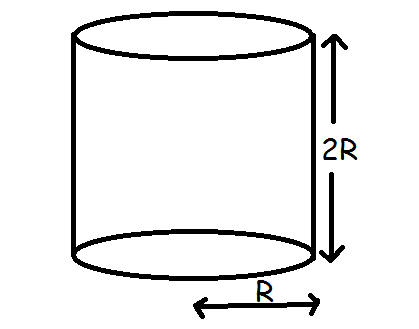 A cylindrical container of dimensions shown in figure has fluid filled completely.
A cylindrical container of dimensions shown in figure has fluid filled completely.
The container is rotated about its axis about angular velocity ω .
Find the angular velocity ω , such that 4 1 of the base of container is visible.
If the answer is of the form ω = b R a g , where a , b are coprime positive integers, find a + b .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions

Did it exactly the same way.To find Height as f{x} was a question I earlier solved in DC Pandey..
Log in to reply
I don't know why these easy questions get level 5. Even moment of inertia which has 400 points was simple as can be seen by my solution
Log in to reply
Not easy for those not who're not preparing for jee perhaps. Moment of inertia was quite easy. I just forgot to take the axis of elementary rings on the inclined axis :p. My question of Geometry has got level 4 which I posted in level 2.
THIS DERIVATION WAS TAUGHT TO ME JUST YESTERDAY
We can consider this problem in another way. We can assume it as a tube with inner radius R/2 and outer radius R. Then simply we have to find the angular velocity for keeping it in equation. It directly jumps down to the last equation.
nyc method
The cylinder is "full": I interpret that as the liquid standing the full height 2 R at the edge of the cylinder.
One quarter of the bottom is visible: thus the liquid reaches height zero at a distance R / 2 from the center.
I use an energy analysis. At the surface the rotating fluid, the total mechanical energy (per unit of mass) is constant. This total energy is a combination of gravitational potential energy ϵ g and kinetic energy ϵ k .
If at a distance r from the axis, the liquid reaches height y , the energy of a unit mass at the surface is ϵ = ϵ g + ϵ k = − g y + 2 1 r 2 ω 2 .
We apply this equation to the liquid at the edge ( r = R ; y = 2 R ) and at the bottom ( r = R / 2 ; y = 0 ): ϵ edge = − 2 g R + 2 1 R 2 ω 2 ; ϵ bottom = 0 + 2 1 ( 2 R ) 2 ω 2 . Equating these gives − 2 g R = − 8 3 R 2 ω 2 , and solving for ω results in ω = 3 R 1 6 g . Clearly, a = 1 6 , b = 3 , and a + b = 1 9 .