Rotating liquid in a bucket
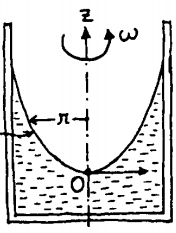
Suppose a bucket contains some incompressible liquid near Earth's surface, where the acceleration due to gravity is g . If the bucket spins with angular velocity ω and we adopt the referential described in the picture (origin O at the free surface and in the axis z and r the distance between the axis and the free surface), the free surface equation (the surface where the pressure equals the atmosphere's pressure) becomes
z A = C g ω B r D ,
where A , B , C and D are the lowest possible integers. Find A + B + C + D .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Hello Zuhair, would you mind developing a little bit more on that derivative? I cant seem to get where you got it from, and why would I use the angle theta for doing so.
Thanks a lot, cheers!
Let p be the pressure at any point inside the liquid. If u is the potential energy density due to all forces acting on the liquid, it is a well-known fact of fluid statics that ∇ p = ∇ ( − u ) . In this case, the liquid spins, but in its own referential, it is static; in this referential, there exists a force density f c = ρ ω 2 r r ^ = − ∇ u c , due to inertial forces. As there's also gravity, the total potential energy density is
u = ρ g z − 2 1 ρ ω 2 r 2 .
As we said before, ∇ p = ∇ ( − u ) , which leads us to the conclusion that
p = 2 1 ρ ω 2 r 2 − ρ g z + c ,
being c some constant. If we let r = z = 0 we are at the surface of the liquid and the pressure must be p 0 , the atmosphere's pressure; this leads to the conclusion that c = p 0 . As we want to find the free surface equation, all we need to do now is let p = p 0 , which gives us
z = 2 g ω 2 r 2 ,
from where we get the sum A + B + C + D .
Lets try it like this. @Lucas Tell Marchi sir's solution is also good but a bit complicated, lets solve it in easier way.
We know for any point on the curve of fluid we have coordinates say ( x , y ) taking (0,0) to be at the minima of the curve.
So we can write that d x d y = tan θ .
Now lets see what forces are acting on the pt mass at (x,y).
Y direction
X direction
Now we know d x d y = g ω 2 x
We can solve this Differential equation and put the limits of x as 0 → r and y as 0 → z .
We will get
z = 2 g ω 2 x 2
⟹ A = 1 , B = 2 , C = 2 , D = 2 ⟹ A + B + C + D = 7