Rotating Rod In Magnetic Field
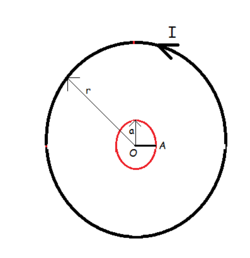 Consider a horizontal circular loop of radius
r
carrying a current
I
. Concentric and coplanar with the loop is a smooth metallic ring of radius
a
, containing a metallic rod
O
A
of mass
m
, as shown. The rod can freely rotate about
O
, the center of arrangement. Between
O
and the circumference of ring, a resistor load
R
(not shown in the figure) is connected, which doesn't obstruct the motion of rod. The rod is given an angular velocity
ω
0
. Find an expression for the maximum angle
θ
through which the rod rotates, if
a
<
<
r
.
Consider a horizontal circular loop of radius
r
carrying a current
I
. Concentric and coplanar with the loop is a smooth metallic ring of radius
a
, containing a metallic rod
O
A
of mass
m
, as shown. The rod can freely rotate about
O
, the center of arrangement. Between
O
and the circumference of ring, a resistor load
R
(not shown in the figure) is connected, which doesn't obstruct the motion of rod. The rod is given an angular velocity
ω
0
. Find an expression for the maximum angle
θ
through which the rod rotates, if
a
<
<
r
.
Find the value of 2 ∣ ∣ ∣ ∣ ∣ ( θ − 3 1 6 R m ω 0 ( μ 0 I a r ) 2 ) ∣ ∣ ∣ ∣ ∣ for the values given below :
Details and assumptions
The resistances of the rod and ring can be neglected.
m
=
1
g
R
=
1
Ω
ω
0
=
1
r
a
d
/
s
r
=
1
m
a
=
1
c
m
I
=
1
0
0
0
A
μ
0
=
4
π
×
1
0
−
7
H
/
m
The answer is 10132.12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Discussions for this problem are now closed
Good solution, but I think this solution of mine is a bit longer than yours.
When I started writing the solution, I thought that I would be explaining everything, but couldn't. I didn't write everything here in the solution like you did there. Almost everything above is mathematical. There are less statements. This one is surely a lengthier problem. Making this was way more fun(and hard) than making that. Btw your solution there is admirable!
Thanks
Sorry, but I think there is a problem with the approximation you made:
( 1 − 2 r x cos θ + r 2 x 2 ) − 3 / 2 ≈ ( 1 + 3 r x cos θ − 2 3 r 2 x 2 cos 2 θ )
where you use ( 1 + x ) n ≈ 1 + x n with x < < 1
but you made the approximation to the power of two r 2 x 2 , so it should be:
( 1 + x ) n ≈ 1 + n x + 2 n ( n + 1 ) x 2 .
Therefore, the approximation should be:
( 1 − 2 r x cos θ + r 2 x 2 ) − 3 / 2 ≈ ( 1 + 3 r x cos θ − 2 3 r 2 x 2 + 2 1 5 r 2 x 2 cos 2 θ )
Yep! you are true . Thanks for pointing that out. That extra cos 2 θ with 2 3 r 2 x 2 was typo, while missing the 2 1 5 r 2 x 2 cos 2 θ term was a mistake. I have edited both the problem and solution.
By the way did you mean ( 1 + x ) n = 1 + n x + 2 n ( n − 1 ) x 2 ?
This gives coefficient of x 2 for n = − 2 3 as 2 − 3 / 2 ( − 5 / 2 ) = 8 1 5 . Hence, in our case the we get 8 1 5 ( 2 r x cos θ ) 2 = 2 1 5 r 2 x 2 cos 2 θ
Yes, sorry, I meant 2 n ( n − 1 )
This is going to be one of the lengthiest solutions you have ever seen on brilliant.
I would be repeatedly using ( 1 + α ) n ≈ 1 + n α for α < < 1
Consider a small element subtending an angle d θ at center as shown. Due to all such elements, magnetic field is in same direction and we can directly sum their magnitudes.
Using cosine formula in △ O P Q ,
y 2 = r 2 + x 2 − 2 r x cos θ
cos ϕ = 2 r y r 2 + y 2 − x 2 = 2 r y r 2 + r 2 + x 2 − 2 r x cos θ − x 2 = y r − x cos θ
Now, using Biot savart law,
d B = 4 π y 2 μ 0 I r d θ cos ϕ
d B = 4 π ( r 2 + x 2 − 2 r x cos θ ) 3 / 2 μ 0 I r ( r − x cos θ ) d θ
B = 4 π μ 0 I r ∫ 0 2 π ( r 2 + x 2 − 2 r x cos θ ) 3 / 2 r − x cos θ d θ
Using approximation for x < < r , we can show that
B ≈ 4 π r μ 0 I ∫ 0 2 π ( 1 − r x cos θ ) ( 1 + 3 r x cos θ − 2 3 r 2 x 2 + 2 1 5 cos 2 θ ) d θ = 2 r μ 0 I ( 1 + 2 3 r 2 x 2 )
Now, emf induced in the rod is ϵ = ∫ 0 a B ω x d x
= 2 r μ 0 I ω ∫ 0 a x ( 1 + 2 3 r 2 x 2 ) d x
= 4 r μ 0 I ω a 2 ( 1 + 4 3 r 2 a 2 )
Now, the current induced is i = R ϵ = 4 R r μ 0 I ω a 2 ( 1 + 4 3 r 2 a 2 )
Now, the torque due to magnetic field on the rod is τ = ∫ 0 a i B x d x
= 4 r μ 0 I i a 2 ( 1 + 4 3 r 2 a 2 )
= 1 6 r 2 R μ 0 2 I 2 a 4 ω ( 1 + 4 3 r 2 a 2 ) 2
⇒ τ ≈ 1 6 r 2 R μ 0 2 I 2 a 4 ω ( 1 + 2 3 r 2 a 2 )
Now, Clearly, τ is decreasing angular velocity. Hence,
− 3 m a 2 ω d θ d ω = 1 6 r 2 R μ 0 2 I 2 a 4 ω ( 1 + 2 3 r 2 a 2 )
⇒ d ω = − 1 6 m r 2 R 3 μ 0 2 I 2 a 2 ( 1 + 2 3 r 2 a 2 ) d θ
⇒ ∫ 0 θ d θ = − ∫ ω 0 0 3 1 6 m R ( μ 0 I a r ) 2 ( 1 − 2 3 r 2 a 2 ) d ω
⇒ θ ≈ 3 1 6 R m ω 0 ( μ 0 I a r ) 2 ( 1 − 2 3 r 2 a 2 )
Hence, θ − 3 1 6 R m ω 0 ( μ 0 I a r ) 2 = ( μ 0 I ) 2 − 8 R m ω 0
Put values to get answer as 1 1 0 3 2 . 1 2