Rotating the Pentagon
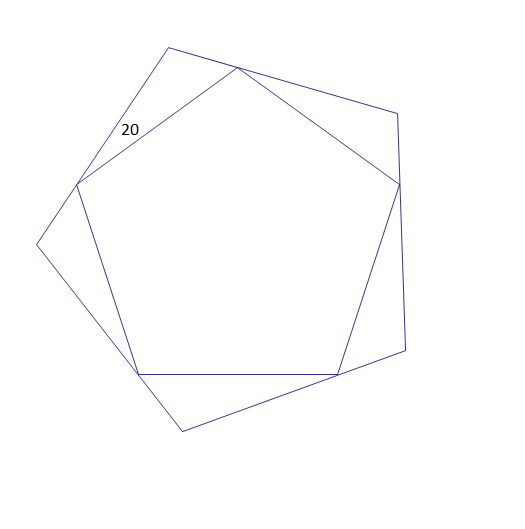 Two regular pentagons are as shown in the figure. The larger pentagon has been rotated
counter-clockwise with respect to the smaller pentagon, such that all the vertices of the smaller pentagon lie on the sides of the larger pentagon, as shown.
Two regular pentagons are as shown in the figure. The larger pentagon has been rotated
counter-clockwise with respect to the smaller pentagon, such that all the vertices of the smaller pentagon lie on the sides of the larger pentagon, as shown.
By what percentage is the larger pentagon's side length larger than the side length of the smaller pentagon?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Is there a way to solve it without a calculator?
My logic:
Let a be the smaller part of the bigger side.
Let b the bigger part of the bigger side.
Let c be the smaller side.
Answer = c a + b
Note that the internal angle of a regular pentagon is n ( n − 2 ) ⋅ 1 8 0 ∘ = 5 ( 3 ) ⋅ 1 8 0 ∘ = 1 0 8 ∘
Then apply the law of sines.
a sin ( 2 0 ∘ ) = b sin ( 5 2 ∘ ) = c sin ( 1 0 8 ∘ )
Rearranging:
c sin ( 1 0 8 ∘ ) sin ( 2 0 ∘ ) ⋅ ( c ) + sin ( 1 0 8 ∘ ) sin ( 5 2 ∘ ) ⋅ ( c ) = sin ( 1 0 8 ∘ ) sin ( 2 0 ∘ ) + sin ( 1 0 8 ∘ ) sin ( 5 2 ∘ )
≅ 1 . 1 8 8 1 8 4 8 0 0 3 4 6 4 9 5 6 0 3 6 1 2 8 4 6 6 4 3 2 2 2 6 4 4 4 4 9 3 2 2 8 9 3 0 3 2 8 7 7 9 3 2 5