Rotating turntable with a ball
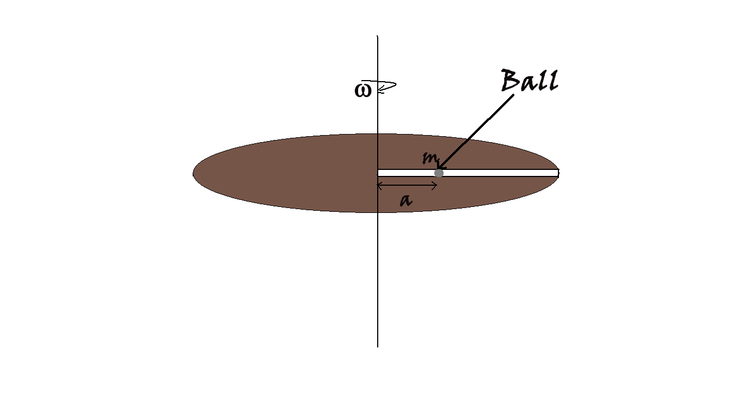 The turntable shown in figure is rotated with constant
rad/sec. A ball of mass 3 kg is gently placed in a frictionless tunnel at a distance
m from the center. Find the radial velocity of ball (in m/s) when it reaches at the end of the tunnel provided, the length of the tunnel is 14 m.
The turntable shown in figure is rotated with constant
rad/sec. A ball of mass 3 kg is gently placed in a frictionless tunnel at a distance
m from the center. Find the radial velocity of ball (in m/s) when it reaches at the end of the tunnel provided, the length of the tunnel is 14 m.
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We know that
F = d p / d t = m d v / d t = m d v / d t d x / d x = m d x / d t d v / d x = m v d v / d x
And the radial force normal is
F = m V 2 / x = m w 2 x
Equaling these equations we get
v d v / d x = w 2 x so v d v = w 2 x d x
Integrating in both sides
v 2 = w 2 ( R 2 − R 0 2 ) V = w R 2 − R 0 2 = 2 6 m/s