Rotating Vessel- Part II
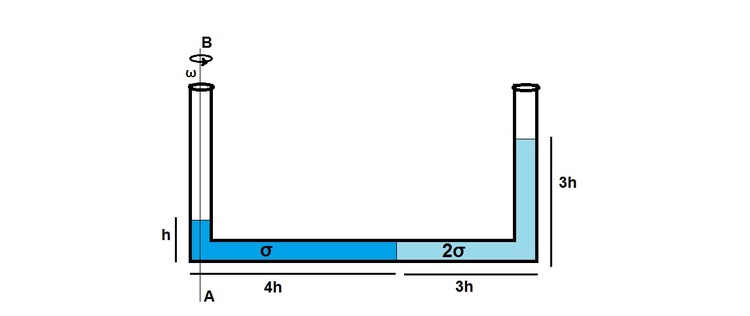 This Problem is a little harder than the previous version, "Rotating vessel". A U-Shaped vessel containing 2 liquids of varying densities σ and 2σ is rotated about the axis AB so that the arrangement in the picture takes place. The height of liquid of density σ is h and that of density 2σ is 3h. The whole horizontal length of the tube is 7h out of which 4h is occupied by liquid of density σ. Find the angular velocity ω with which the tube is rotated.
This Problem is a little harder than the previous version, "Rotating vessel". A U-Shaped vessel containing 2 liquids of varying densities σ and 2σ is rotated about the axis AB so that the arrangement in the picture takes place. The height of liquid of density σ is h and that of density 2σ is 3h. The whole horizontal length of the tube is 7h out of which 4h is occupied by liquid of density σ. Find the angular velocity ω with which the tube is rotated.
Note:
g
=
1
0
m
/
s
2
h
=
4
1
2
m
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
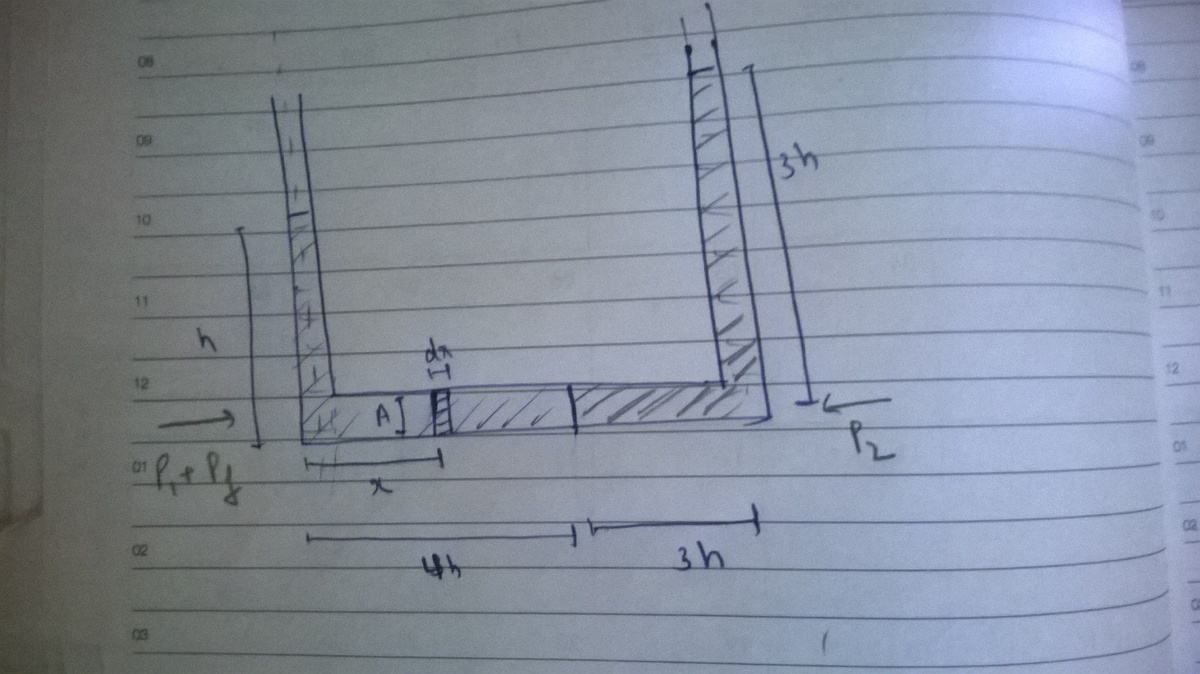

Did the same!
let us consider two corners A and B.
now at corner B,
P
1
=
P
2
+
P
3
.
P
1
is the pressure due to the part of the liquid of density
2
σ
which is at a height of 3h.
P
2
is the combined pressure of liquids due to rotation which is situated horizontally.
P
3
is the pressure due the to part of the liquid of density
σ
which is at a height of h.
so,
2
σ
g
(
3
h
)
=
[
8
σ
h
2
ω
2
+
σ
3
3
h
2
ω
2
]
+
σ
g
h
.
for calculating the pressure due to rotation due to the liquids situated horizontally, distance of the centre of mass of both the liquids from the rotational axis should be taken as the radius of rotation. first calculate the centrifugal force and then divide it by area to get the pressure
Please tell me about pressure due to horizontal liquid
Log in to reply
Find the mass of both the liquids in terms of area A and then find the distance of com of both the liquids. now consider them two point masses rotating about the axis. Find the centrifugal force and divide it by area. So finally u get the pressure
