Rotating Vessel
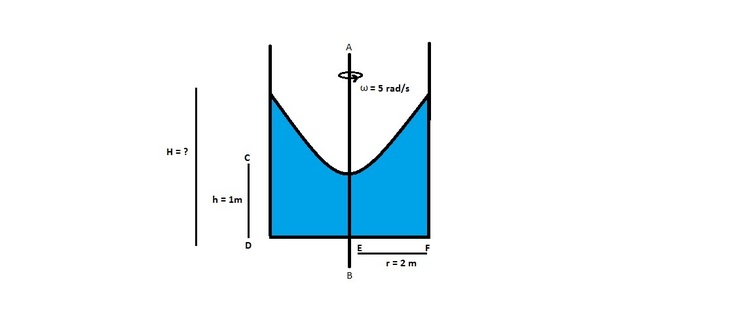 A vessel of radius
r
is rotated about the axis AB with angular velocity
ω
such that the lowest point of the water surface is at a distance of 1
m
from the bottom. Find the distance
h
of the highest point of water level from the base. Assume that no water flows out of the vessel.
A vessel of radius
r
is rotated about the axis AB with angular velocity
ω
such that the lowest point of the water surface is at a distance of 1
m
from the bottom. Find the distance
h
of the highest point of water level from the base. Assume that no water flows out of the vessel.
Details
- R = 2 m
- ω = 5 rad/s
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
why are we using Fsin¢=mw^2x??
Log in to reply
Consider,the coordinate axis along the line parallel to the side of the container {taken as y axis}& the horizontal line through the point {that point where the considered mass is situated} taken as x axis.[ I mean two perpendicular lines through that point]
Let, the force F makes an angle ¢ with the y axis. This means
Fcos¢ ballances mg& Fsin¢ ballances the centrifugal force mw^2x.
As the force makes an angle ¢ with the vertical, the tangent of the curve (water surface) makes the same angle with the x axis .So tan¢=dy/dx
(I think it is the sufficient explanation for you)
Formula for the question is
Y= 2 g R 2 w 2 + \y m i n Substitute the given values in formula you get y minimum is 1 metre in the question
from where did u get this formula...can u derive it..please!!
wow. I derived this formula but for some reason ended up with 4g in the denominator instead of 2g.
dy/dx=w^2x/2g.THEN integrate it.
Log in to reply
Sorry.I made mistake while writting.But I SOLVED IT RIGHT.
how can we use pressure method?i mean pressure at the lowest point and that at the same level vertically below the curved point?
Applying Bernoulli's equation considering two points : one at the vertex of parabola and one at the edge of the tube where water is at highest position.
You will get h ′ = 5 m , h ′ → height with respect to vertex of parabola.
Means from base it is 5 + 1 = 6
H(max)=h(min)+ (w^2).)R^2)/2g : g is acceleration due to gravity= 10m/s -->H = 1+ (5x5)(2x2)/2x10 ---> = 6
At first find the pressure on both the ends of the tube. Substrac two equations to get this formula H-h=w^2/2g(R^2). put the values and get the answer!
Fine!!! A new corner of thinking!!!!!!!!!!
Why is it that w^2*x is equivalent to acceleration Thanks
(5^2)(2^2)/2(9.81)=5.097+1=6.097 or 6.1 to be exact..
Let, consider a point on the curved surface of water.
Let , the mass of the point is m.
The force acted on the mass m is F which makes an angle ¢ with the vertical
So that Fcos¢=mg
F s i n ¢ = m w 2 x
t a n ¢ = w 2 x / g
d y / d x = w 2 x / g
Y = w 2 × x 2 / 2 g [integrating both side]
Y = 5 m w = 5 , x = 2 , g = 1 0
The height of the highest point from the base is =5+1=6m