Rotation 4
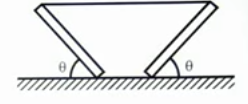
The figure above shows 2 identical planks, each of which makes an angle of with the rough horizontal surface. A string holds these 2 planks together at the top.
Given that the coefficient of static friction between each of the planks and the surface is 0.5, find the minimum (in degrees, to 1 decimal place) for which the system will remain in an equilibrium state.
The answer is 45.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Torque - Equilibrium
Since both sides are symmetric w.r.t. a vertical axis passing through the center of the string, we'll focus on only one of the planks.
The forces operating on this plank are showing in the diagram above where T is the tension in the string, m g is the gravitational force acting upon the center of mass of the plank, N is the normal reaction force and f is the force of friction between the plank and the surface of the ground.
Balancing forces in vertical direction, we have
N = m g .
Since T is unknown, it's best to balance torque about point O . Thus we have
m g ( 2 ℓ cos θ ) − N ( ℓ cos θ ) + f ( ℓ sin θ ) = 0 ⟹ m g ( 2 ℓ cos θ ) − m g ( ℓ cos θ ) + f ( ℓ sin θ ) = 0 ⟹ tan θ = 2 f m g
For minimum tan θ , f should be maximum.
From the condition of no slipping, we know that
f ≤ f max possible ⟹ f ≤ μ m g
Thus maximum value of f is μ m g . Hence minimum value of tan θ is
tan θ = 2 μ m g m g = 2 μ 1 = 2 × 0 . 5 1 = 1 .
As we know that for θ ∈ [ 0 , 2 π ] , θ decreases as tan θ decreases, so
θ min = arctan ( 1 ) = 4 5 ∘ .