Rotation is Fun!
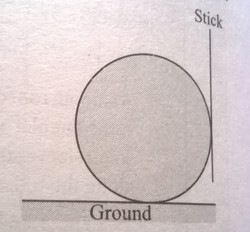A boy is pushing a ring of mass 2 kg and radius 0.5 m with a stick as shown in the figure. The stick applies a force of 2N on the ring and rolls it without slipping with an acceleration of 0.3
. The coefficient of friction between the ground and the ring is large enough that rolling always occurs and the coefficient of friction between the stick and the ring is
. Then the value of p is?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
We have Fs=2N(right to left) force from the stick. The ground applies a force Fg(left to right) which is unknown and there is a force Ts(up to down) from the stick to the ring which is parallel to the stick and is the friction of the stick with the ring. Fs,Fg are applying linear motion acceleration while Ts and Fg apply angular acceleration. We use the Newton's law F=m a for the linear acceleration, so we have Fs-Fg=m * a => 2-Fg=2 * 0.3 => Fg=1.4N, We now use Newton's law for angular acceleration T=A_ang I
we have a ring so I = m *r^2, A_ang= R a
so (Fg-Ts) * R= R a * m * R^2 => Fg-Ts=m * a => 1,4-Ts=2 * 3 => Ts=0.8 N But the Ts which is the friciton is equal to the coefficient of friction multiplied but the stick force. so Ts=p/10 * 2 => 0.8=p * 2/10 => p=4