Rotation, rotation, rotation!

Here's a solution in terms of complex numbers

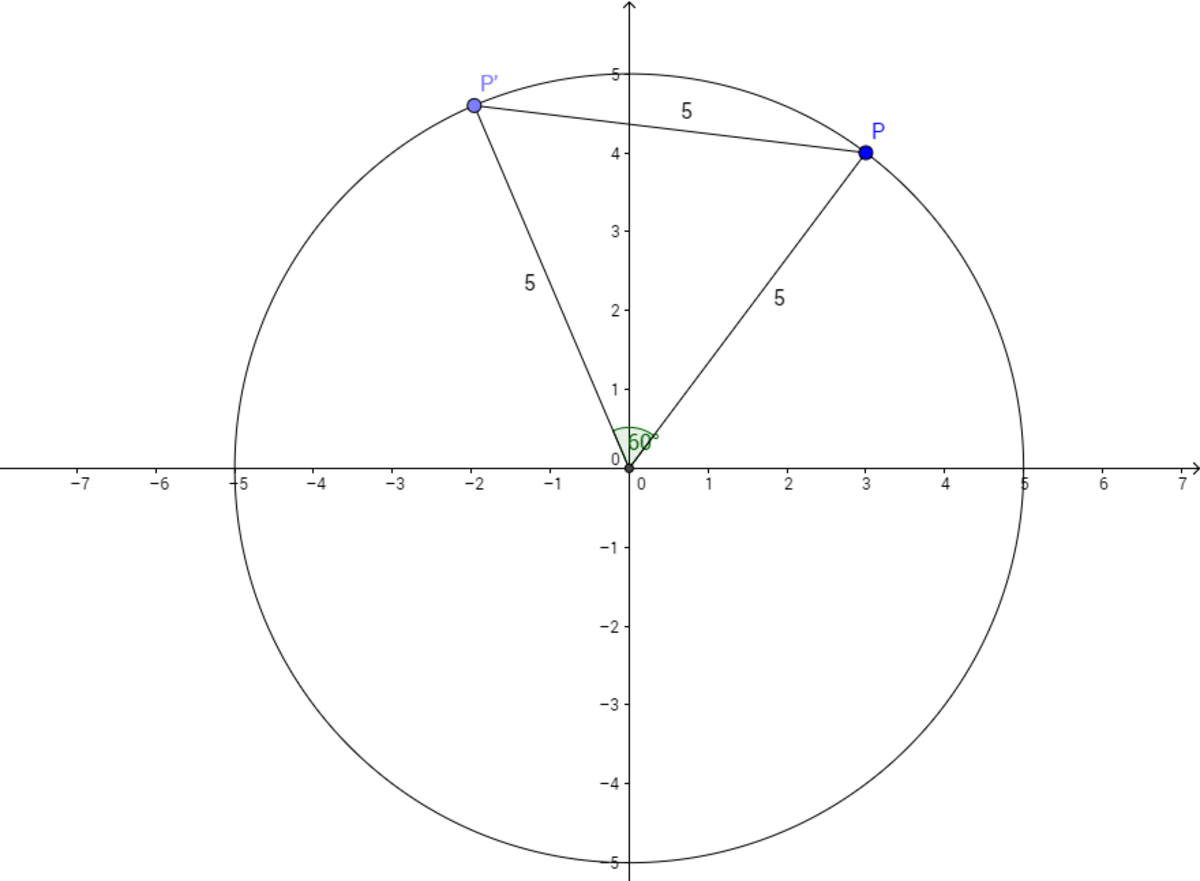All lengths are in units, and all angles are in degrees.

In the diagram, $P'$ refers to point $P$ following the rotation. It can be observed that a triangle is formed between $P$ , $P'$ , and $(0, 0)$ . Because the equation of the circle on which $P$ 's rotation path lies is $x^{2} + y^{2} = 25$ , the radius must be $5$ units, meaning that the two sides of the triangle meeting at $(0, 0)$ are length $5$ units. Because the angle between them is $60°$ , it follows that the triangle is equilateral. Therefore, $\overline{PP'} = 5$ . If the coordinates of $P'$ are $(x, y)$ , then we can set up an equation $(x-3)^{2} + (y-4)^{2} = 25$ . We now have two equations:

$x^{2} + y^{2} = 25$

$(x-3)^{2} + (y-4)^{2} = 25$

Solving for $x$ and $y$ reveals that $x = \frac{3}{2} - 2\sqrt{3} \approx{-1.96}$ and $y=2+\frac{3\sqrt{3}}{2}\approx{4.6}$ . Adding the two gives us $\boxed{2.64}$ .