Rotational Mechanics
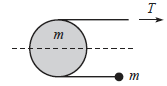 A solid cylinder of mass
and radius
lies flat on friction less horizontal table, with a mass less string running halfway around it, as shown in figure. An object also of mass
is attached to one end of the string, and you pull on the other end with a force
. The circumference of the cylinder is sufficiently rough so that the string does not slip with respect to it. What is the acceleration of the mass m attached to the end of the string?
A solid cylinder of mass
and radius
lies flat on friction less horizontal table, with a mass less string running halfway around it, as shown in figure. An object also of mass
is attached to one end of the string, and you pull on the other end with a force
. The circumference of the cylinder is sufficiently rough so that the string does not slip with respect to it. What is the acceleration of the mass m attached to the end of the string?
Note : Give your answer with magnitude and direction. Choose right side to be positive and left side to be negative.
Also try my set .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First we have to draw FBDs.
So ( T + F ) = m a ..........................(1)
Let the angular acceleration of pulley be α in clockwise direction. Let clockwise direction be positive
So ( T − F ) r = I α
Here I = 2 m r 2
So α = m r 2 ( T − F ) ........(2)
Now we will get other equation be equating accelerations at the point of contact of cylinder and string.
Let the point 1 be on the string and point 2 be on the pulley. As the string is not slipping so acceleration of point 1 and 2 are equal.
Also acceleration of point 1 is equal to the acceleration of object.
Let a 1 be the acceleration of the object.
So a 1 = m F .........................(3)
NOTE- The acceleration of the object will be towards left.
Now point 2 has two accelerations
1) Due to translation which is equal to a towards right
2) Due to rotation which is equal to r α towards left.
Let us assume right side to be positive and left side to be negative.
Then − a 1 = a − r α
So m F = m r 2 ( T − F ) − m T + F
So F = 4 T ..............(4)
Now from eq(3)
a 1 = − m F
From eq(4)
a 1 = − 4 m T