Rotational Motion At Its Best !

A uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes angle θ with the horizontal.
The answer can be expressed in the form of ( b + d c o s 2 θ ) a g l ( 1 − s i n θ ) c o s 2 θ where a,b,d are positive integers. and b,d are co-prime
Find value of a+b+d ?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Aditya , I have Added an Diagram for Your Question , Please Tell me is it ok or not ? If You Have any issues Than tell me !
Log in to reply
That's my question Falling Stick
Well I had the advantage since I already the knew the answer in advance.
Nice solution bro and a nice use of ICR concept!
I think you love to use ICR concept for solving problems. :D
Log in to reply
Yes I Love This Technique , Because it Helps when Situation are complex ! So It is in my Habit ! But Your's is also Nice
Thnxx bro for nice solution..🐼
We can get a equation from the conservation of energy.
2 m g l ( 1 − s i n θ ) = 2 m v 2 + 2 I ω 2
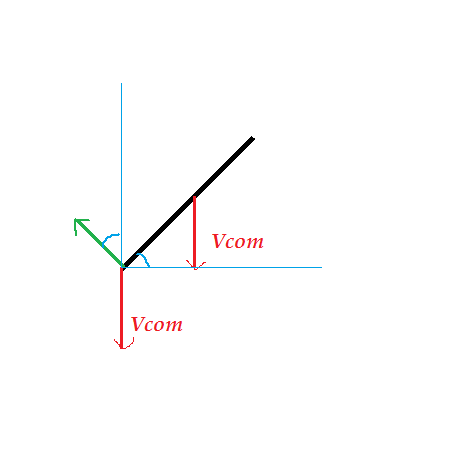
Here green arrow shows the velocity of the lower end of the rod due to the rotation.
Velocity of the lower end of the rod in vertical direction is zero .
So V c o m = 2 l ω c o s θ
Using these two equations we get
V = 3 c o s 2 θ + 1 3 c o s 2 θ ( 1 − s i n θ ) g l
Could u help me find the he normal reaction at this instant
We will Do This Question By ICR Instantaneous Centre of Rotation
Since There is No Horizontal Force on Rod So Centre of mass of Rod will fall vertically Downward only (Does not have any Horizontal Velocity) So We Locate ICR of This Rod By Taking Intersection Point of perpendicular Lines drawn two two velocity as Shown in figure ! And In ICR frame Rod is in Pure Rotational Motion So we can use Energy Conservation in ICR frame!
2 m g L ( 1 − sin θ ) = 2 1 I i c r ω 2 2 m g L ( 1 − sin θ ) = 2 1 m ( 1 2 L 2 + 4 L 2 cos 2 θ ) ω 2 ω = L ( 1 + 3 cos 2 θ ) 1 2 g ( 1 − sin θ ) V c m = ω 2 L cos θ V c m = ( 1 + 3 cos 2 θ ) 3 g L ( 1 − sin θ ) cos 2 θ .
Q.E.D