Rotavirus
Rotavirus has many variations. All the variations are generated from a wheel, which contains a cycle of nodes, with an extra node connected to each one on the cycle, as shown in the picture:
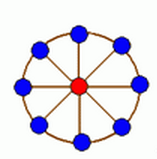
All the valid rotaviruses are formed by breaking some edges from the wheel, such that every two nodes have
one and only one path
to reach each other. When
, there are
different valid rotaviruses:
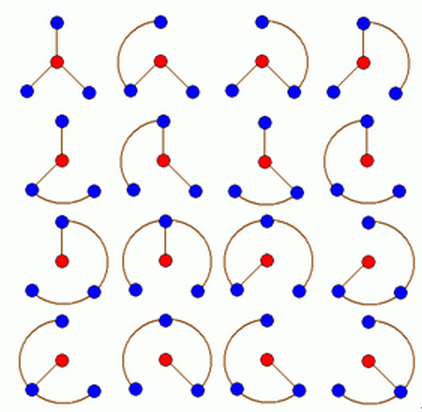
For a wheel containing a cycle of nodes, there are different rotaviruses to generate from.
How many digits are in expressed in base
This problem was inspired by the popular weekly problem .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Treat the rotavirus as a labelled graph on N + 1 vertices. By the matrix tree theorem, the number of spanning trees of the graph is given by
∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 3 − 1 0 ⋮ − 1 − 1 3 − 1 ⋮ 0 0 − 1 3 ⋮ 0 0 0 − 1 ⋮ 0 ⋯ ⋯ ⋯ ⋮ ⋯ 0 0 0 ⋮ − 1 − 1 0 0 3 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣
If we call the above determinant A N , then we get, after "some" algebraic manipulations, A N = L 2 N − 2 where L k is the k th Lucas number. Thus
A 1 0 0 = ( 2 1 + 5 ) 2 0 0 + ( 2 1 − 5 ) 2 0 0 − 2 which has 4 2 digits.
Honestly, this is Discrete Mathematics.