Round about

Let the particle travels such that the thread wraps on the cylinder by an angle $\theta$ in time t.
At any time instant the velocity of the particle is perpendicular to the thread, hence it will not do any work on the particle and its kinetic energy and speed will remain constant.
After time t, the length of the thread which is not yet wrapped will be $r=L-R\theta$ .
Differentiating with respect to time, we get
$\frac{dr}{dt}= - R\frac{d\theta}{dt}$
$d\theta = - \frac{dr}{R}$
The distance moved by the particle in further small time ‘dt’ will be $vdt = r d\theta$
Replacing the value $d\theta = - \frac{dr}{R}$
$vdt = -\frac{rdr}{R}$
$\begin{gathered} v\int_0^t {dt} = - \frac{1}{R}\int_L^0 {rdr} \\ t = \frac{{{L^2}}}{{2vR}} \\ \end{gathered}$

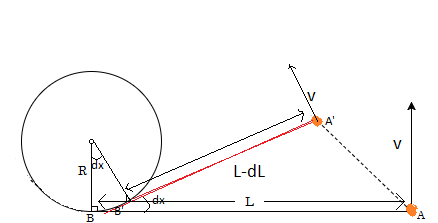
Careful observation will show that angular momentum is not conserved about any feasible point due to tension in thread.Also velocity will remain conserved because tension is perpendicular to motion of particle.

Let particle reach position A' in time dt.

Amount of thread wrapped = dL = R(dx) $\cdots \cdots \cdots (\#)$ .

Now since time interval considered is very small,B'A'A is 'almost' a circular arc of radius = L-dL.

AA' =(L-dL)dx= v(dt)

Substituting value of dx from $\#$ ,

v(dt)=dL(L-dL)/R

Since dL times dL is veryy small,we will ignore it.

$\implies vdt = \frac{LdL}{R}$

$\implies vt = \frac{L^{2}}{2R}$

$\implies t = \frac{L^{2}}{2vR}$

A better problem would have been the one in which the cylinder too rotates to conserve the angular momentum,here the cylinder's axis is fixed by external means which is exerting torque,but wouldn't it be nice if the cylinder too is free to rotate due to torque by the tension of the thread about its centre,a popular one this