Round and about
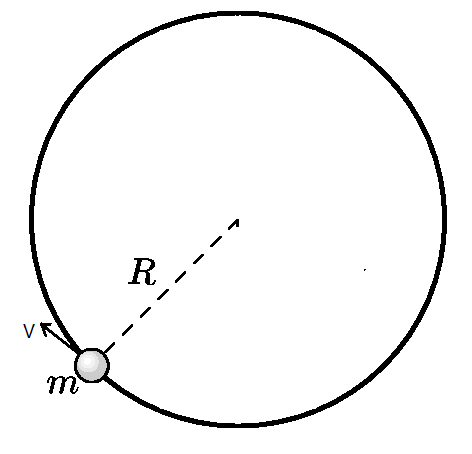
A small bead of mass is given an initial velocity of magnitude on a horizontal circular track of radius . If the coefficient of of kinetic friction is , what is the distance covered by the bead before coming to rest?
Assumptions and Details
- Take acceleration due to gravity as .
- The track goes through a small hole in the bead. The surface of the hole is uniform so that the coefficient of friction is the same in all directions.
The answer is 0.822457.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The working differential equation is m v d s d v = − μ k ( m g ) 2 + ( R m v 2 ) 2 which can be directly solved to get the answer.