Row Across The River

Logic Level 2

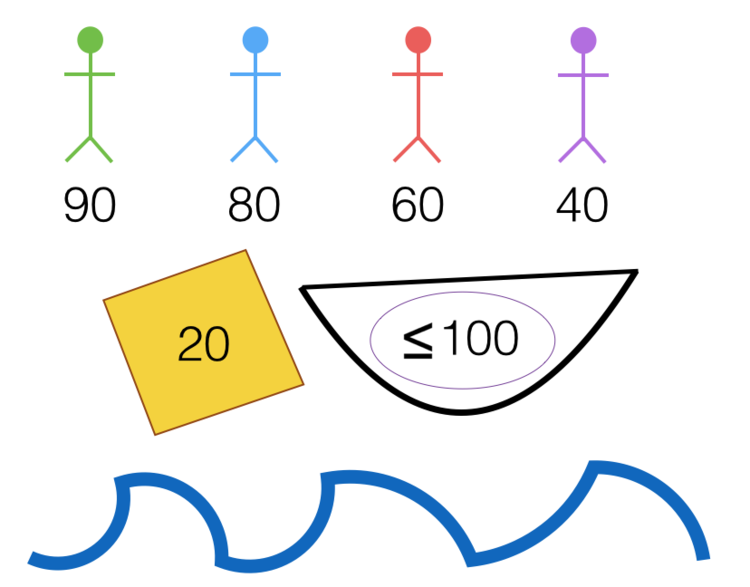Alex, Brook, Chris, and Dusty need to cross a river in a small canoe. The canoe can carry only 100 kg. Alex weighs 90 kg, Brook weighs 80 kg, Chris weighs 60 kg, Dusty weighs 40 kg, and they have 20 kg of supplies.

Find the minimum number of times they have to row across the river so that everyone and the supplies are safely across, assuming that at least one person must be in the rowboat during the trips.

7 9 11 13

View wiki
Anish Harsha by Anish Harsha , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

Anish Harsha
Oct 29, 2015

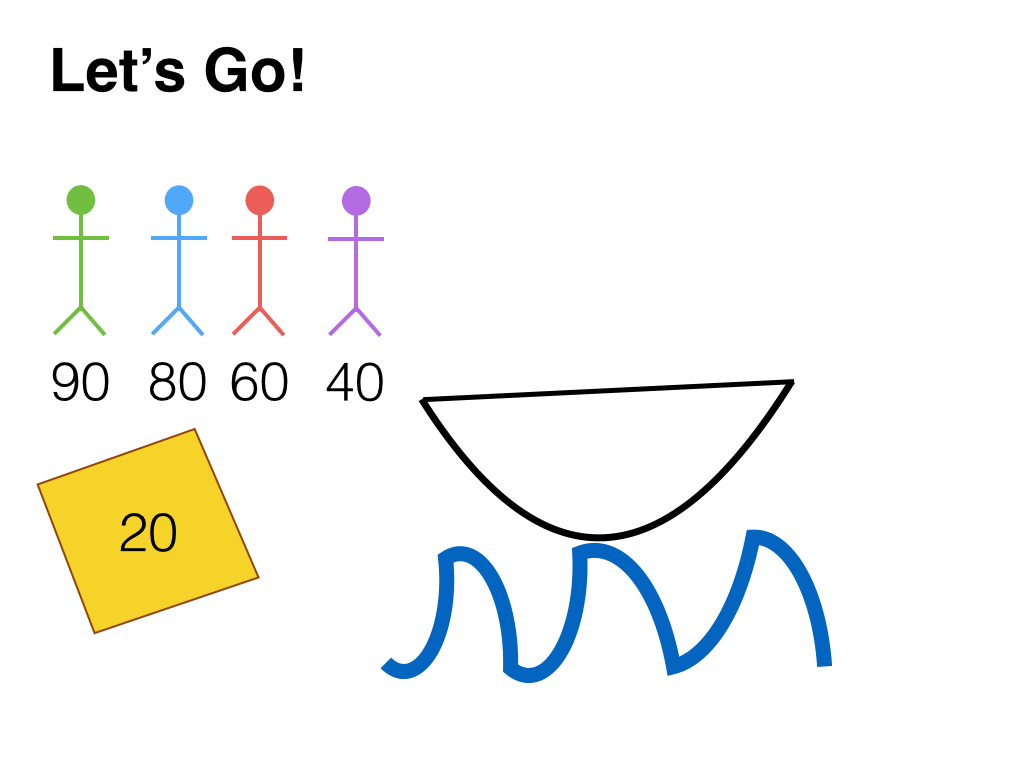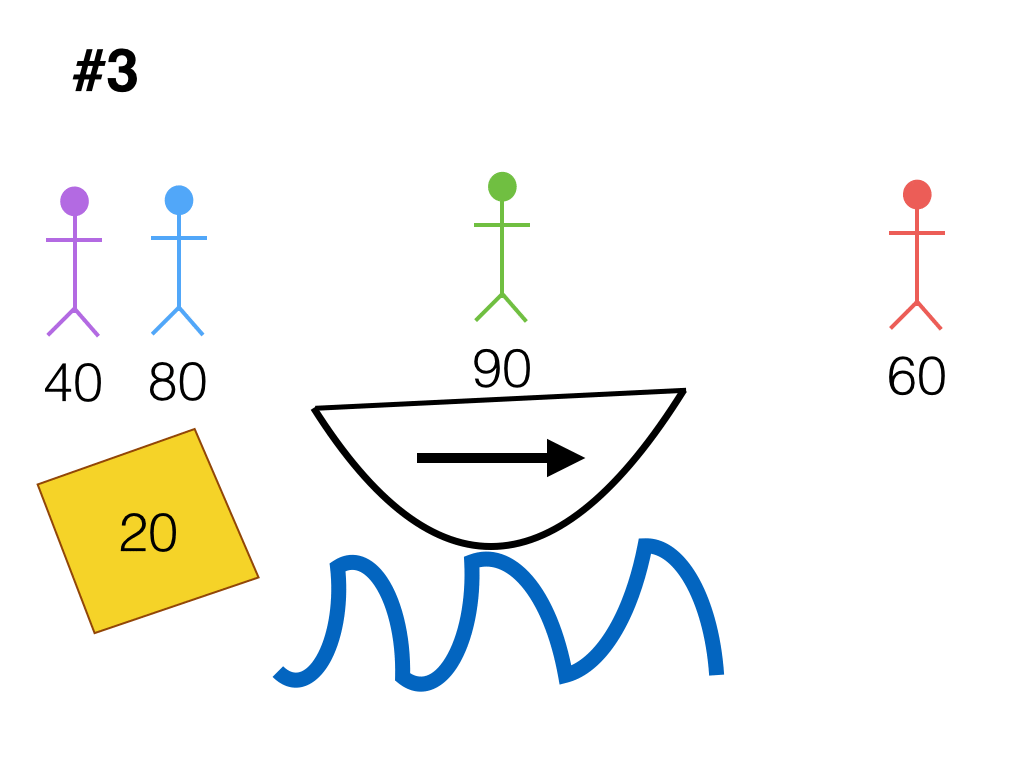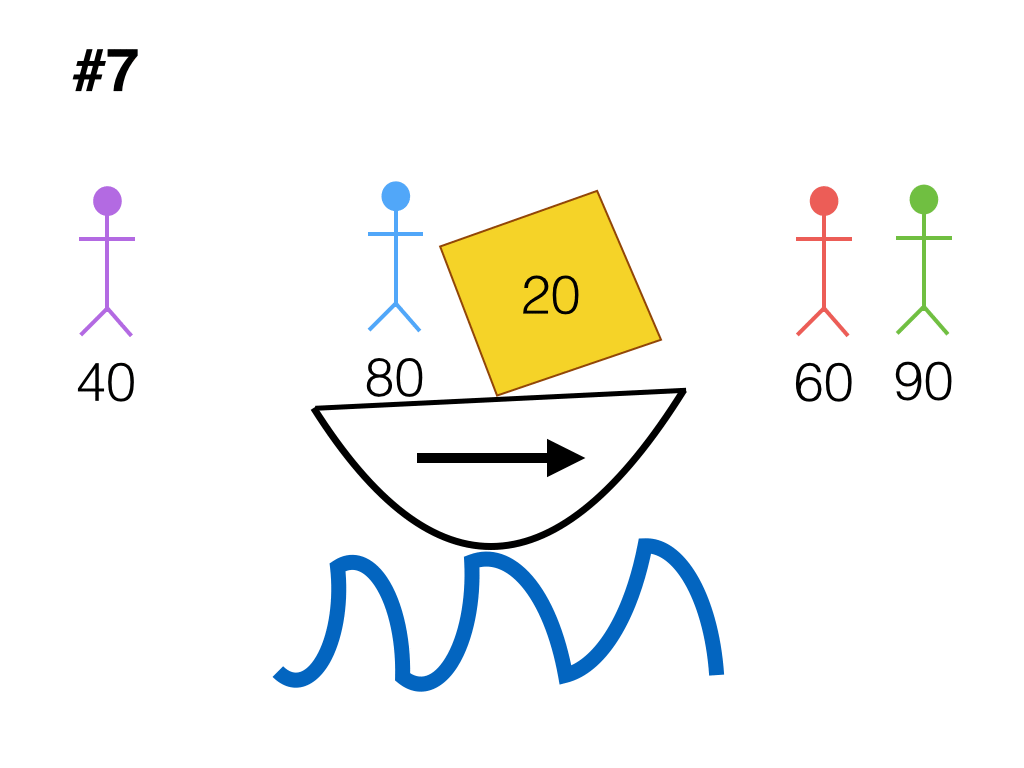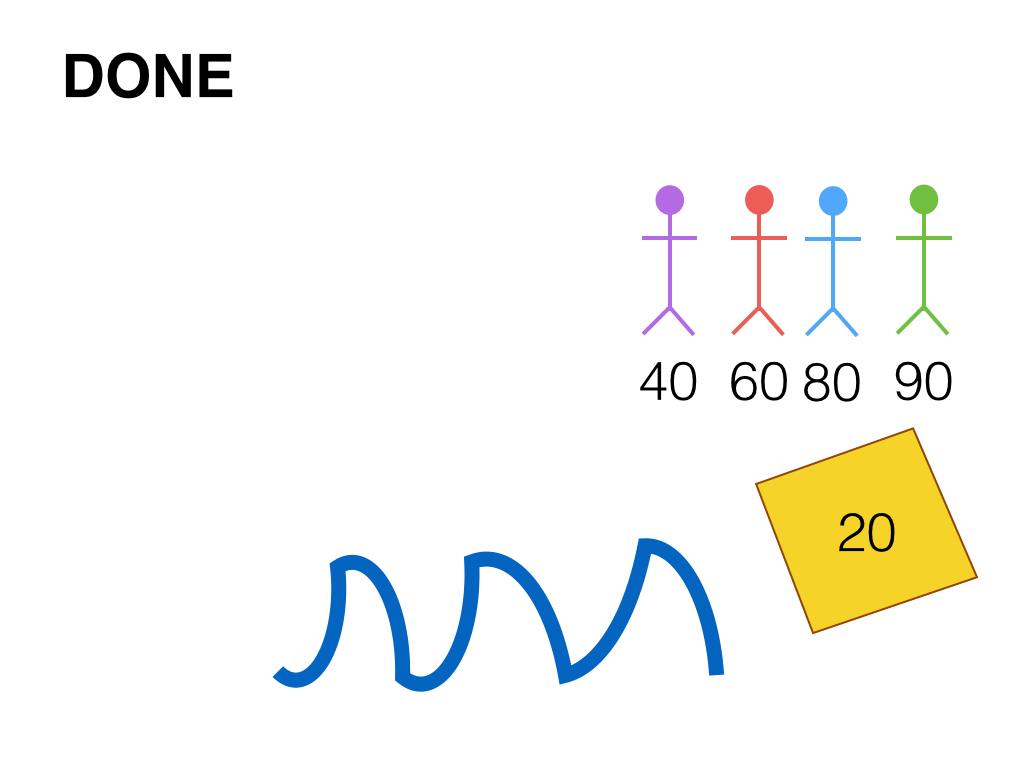
Let's show that it can be done in 9 trips:

  1. Chris and Dusty row across. (100)
  2. Dusty returns. (40)
  3. Alex rows over. (90)
  4. Chris returns. (60)
  5. Chris and Dusty row across again. (100)
  6. Dusty returns. (40)
  7. Brook rows across with the supplies. (100)
  8. Chris returns. (60)
  9. Chris and Dusty row across again for the last time. (100)

It's not too hard to show that it can't be done in 7 (or fewer) trips. Can anyone prove this?

11 Helpful 0 Interesting 0 Brilliant 0 Confused

That's quite clever! If anyone wants to see this in action:

Eli Ross Staff - 5 years, 7 months ago

Alright, to prove that we need to cross at least nine times, we can see that no subset of three elements can fit in the boat, because every three-element subset from {20, 40, 60, 80, 90} has sum of its elements greater than 100. This mean, there can be at most two elements in the boat at any time. Let's say we assign two elements randomly to the boat at every trip (ignoring every other restriction of the problem). The minimum number of trips is 9, because we have 5 elements and the boat needs to end on the right side of the river. That proves that we need at least 9 trips to get everyone to the other side.

Anish has shown that we need at most 9 trips to solve the problem, so we need exactly 9 trips to solve the problem!

Gustavo Rocha - 5 years, 7 months ago

Chris + dusty------------> Chris + dusty 

          dusty<----------- (Chris remain here, dusty went back)

Brook + supplies------------>Brook + supplies +Chris 

          Chris<-------------- (Brook and supplies were left and Chris went back)

Chris + dusty --------------->

So ultimately, in 5 steps only they can cross river.

Swati Verma - 5 years, 7 months ago

Log in to reply

Where is Alex in this solution?

Adam Bachmann - 5 years, 7 months ago
Supriyatna Pri
Oct 30, 2015

Trips;

  1. --> Chris + Dusty (100 kg)

  2. <-- Dusty (40 kg)

  3. --> Brook and supplies (100 kg)

  4. <-- Chris (60 kg)

  5. --> Chris + Dusty (100 kg)

  6. <-- Dusty (40 kg)

  7. --> Alex (90 kg)

  8. <-- Chris (60 kg)

  9. --> Chris + Dusty (100 kg)

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Neeraj Karn
Oct 30, 2015
  1. 60 & 40 go => 60 stays
  2. 40 comes back
  3. 80 & 20 go => both stay
  4. 60 comes back
  5. 40 & 60 go => 40 stays alongwith 80 & 20
  6. 60 comes back
  7. 90 goes => 90:stays alongwith 80 & 20
  8. 40 comes back
  9. 40 & 60 go => all are on the other side.
0 Helpful 0 Interesting 0 Brilliant 0 Confused
Het Naik
Oct 30, 2015

First 60 kg and 40 kg go that side .cross no 1 then 40kg return with boat.cross no 2. Then 90kg go .crooss no 3. 60 kg return. Cross 4. another time 40 and 60 go.cross 5. 40 return. Cross 6. 80 go with 20.cross7. 60 return. Cross8. 60 and 40 go.cross 9.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...