Rows and soldiers
What is the minimum number of soldiers needed to form 1 2 lines of at least 3 soldiers each?
6 soldiers can form 3 lines of 3 soldiers each
Note
: The lines must be distinct. For example, if you have 5 soldiers in a line, this only counts as 1 line.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
This is one of those mathematical problems which have a simple statement, but is actually quite hard to prove.
There is ongoing research by mathematicians like Terence Tao to understand the upper and lower bounds for the general case.
Check out the Open Problems Group if you want more like this.
Your central vertical line now has four soldiers on it... You need to deform this picture a little more.
Log in to reply
The rules say that a line with more than 3 points only counts as one line, But it is not rule breaking if a line has more than 3 points.
Log in to reply
It is a shame. The question contradicts itself. It starts by saying that a line contains 3 soldiers, and then allows more. I think this was an attempt to stop people scoring multiple lines by having many points on the same line.
The question is harder, and more interesting, if you insist that there are only 3 soldiers on any line. You can still get 12 lines with 10 soldiers.
I did consider that, but since the note included in the question clearly implied that it was acceptable for more than three soldiers to be on a line, I chose to go for symmetry rather than restrict the solution to exactly three on each line.
Knowing the 'ten rows of three from nine objects' of old (it is over 30 years since I came across it), I deduced that one extra soldier above the nine if placed correctly could give us 12 rows of three - you have shown one way to do it.
Log in to reply
You're right, of course; I was in no way suggesting this was an original idea of mine, and I've added a note to my solution to make that clear.
I could use 9 but the quiz say incorrect answer.
I also found a solution with 10 dots (shown below), but don't know why 10 is the minimum. Could someone prove that?
Also, the example they gave wasn't the best you can do with six dots:
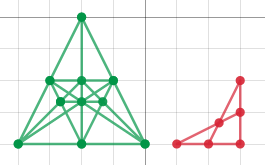
The soldiers define an incidence geometry (See: link text , where lines contain exactly three points. So a minimal solution to a "soldier geometry" with 12 lines is …
Points: 1,2,3,4,5,6,7,8,9,10
Line One: 1,2,3
Line Two: 4,5,6
Line Three: 7,8,9
Line Four: 1,4,7
Line Five: 2,5,8
Line Six: 3,6,9
Line Seven: 4,10,3
Line Eight: 2,10,7
Line Nine: 1,10,5
Line Ten: 1,10,9
Line Eleven: 1,5,9
Line Twelve: 10,5,9
This is illustrated by the following diagram:
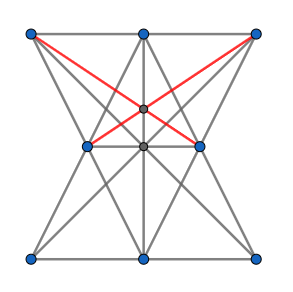
The question does not make it clear whether you are allowed more than three soldiers on a line, or whether each line has to have exactly three soldiers on it... You are getting four lines out of the soldiers numbered 1,10,5,9.
If you are going to allow more than three soldiers on a line, you simply could line up 6 soldiers in a row. Any three of them would form a line, and so you could form ( 3 6 ) = 2 0 lines of three with these six soldiers. That certainly gives you 1 2 lines, but this is not what, I think, the question is looking for (particularly since 6 is not a solution option).
Looked at another way, you are defining line segments rather than (infinitely extended) lines .
There is a segment with 4 points.. this drawing does not fit the problem
What happened to distinct lines?-- you're counting the 1-10-5-9 three ways, the problem doesn't allow that.
It is clear that the problem states that each line must be distinct and you have lines 9,10,11, & 12 that are all just one line (the same line).
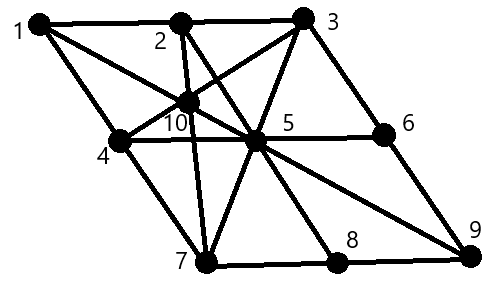
Here is a new proposal, similar to the first proposal but without 4 soldiers line :-)
Brilliant!! but still to be proved 10 is minimum numbers of soldiers.
Log in to reply
You are right I am working to find it, so far I was unnable to crak. The above solution contains only 3 soldiers per line and you can built infinite solutions just starting with two perspective triangles.
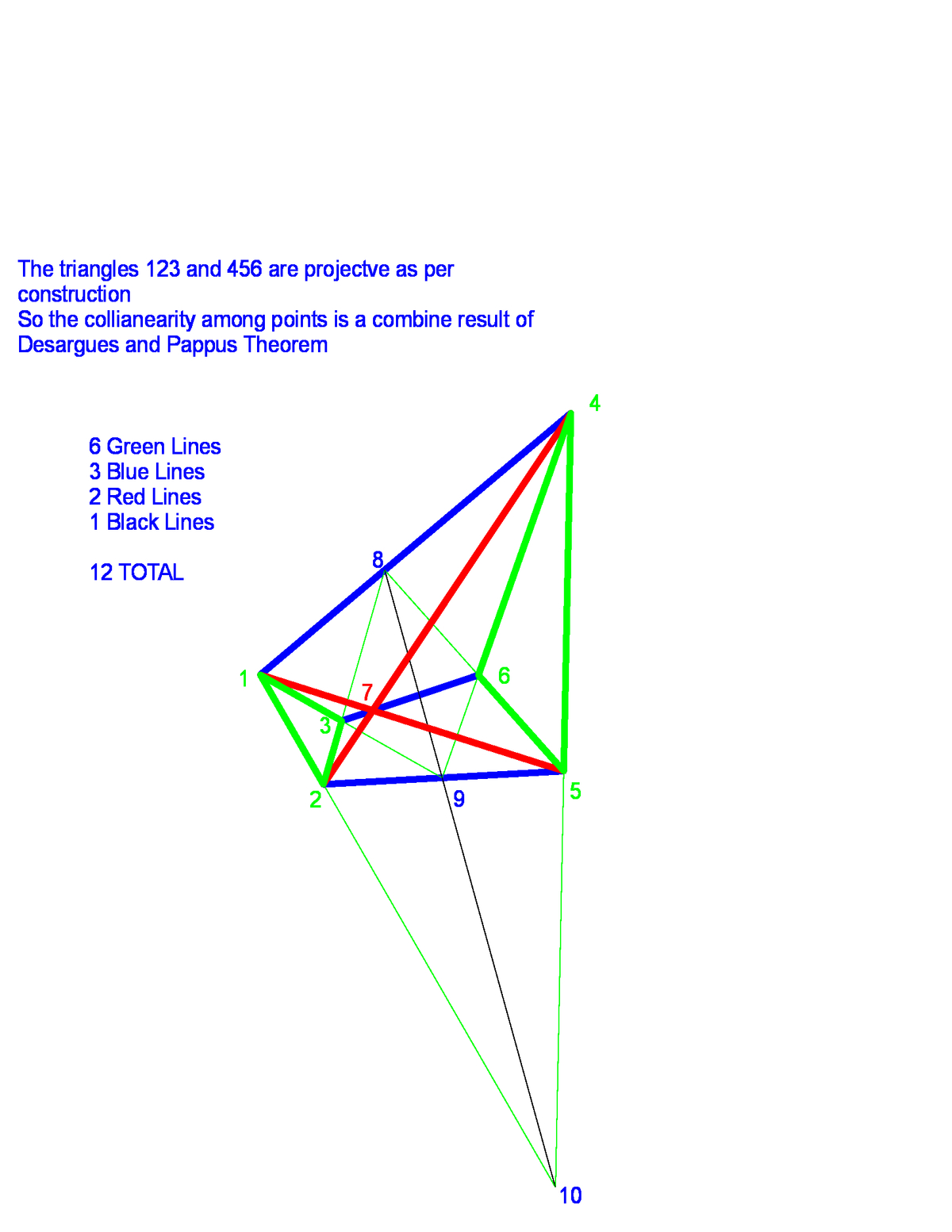
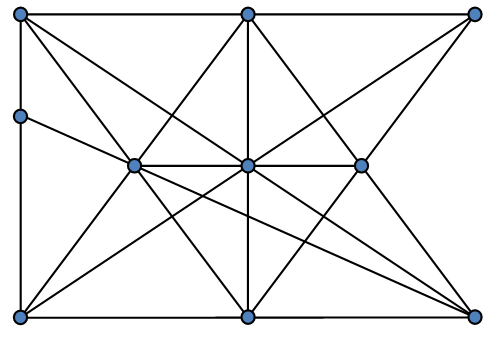
We can arrange ten soldiers and form twelve rows of three soldiers each.
We start by arranging nine soldiers in a 3 by 3 square grid, as shown below. Clearly, they form eight rows of three soldiers each.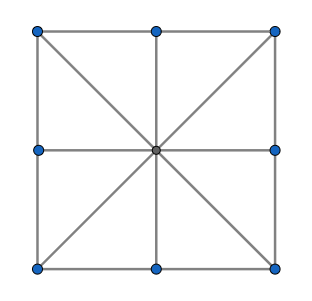 However, we can improve on this number of rows by moving the two soldiers at the ends of the middle row halfway towards the centre soldier. This eliminates the vertical row for each of the moved soldiers, but it creates two additional rows for each, giving us ten rows.
However, we can improve on this number of rows by moving the two soldiers at the ends of the middle row halfway towards the centre soldier. This eliminates the vertical row for each of the moved soldiers, but it creates two additional rows for each, giving us ten rows.
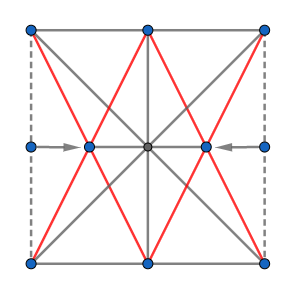 I believe this is the maximum number of rows achievable with nine soldiers, but know of no way to prove this.
I believe this is the maximum number of rows achievable with nine soldiers, but know of no way to prove this.
[None of the above is an original idea, I remember seeing this a few years ago and I'm sure it should be well-documented online.]
Now if we simply add one more soldier at the right spot on the center line, we create two more rows for the requisite twelve.