Rubber Physics (Part 2)
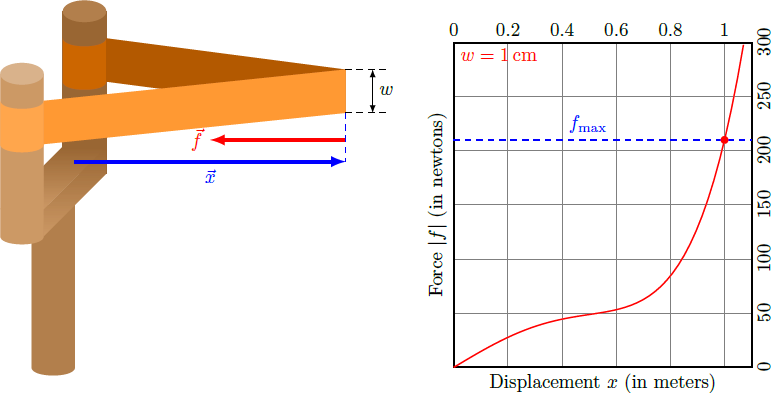
Dennis wants to use his slingshot to fire a ball at the highest possible speed. For selection he has different rubber bands, which are all made of the same material, have the same thickness and length, but differ only in their widths For the rubber band of width the force-distance curve is known and given by a polynomial The graph of this function is plotted in the diagram below. We assume that Dennis tenses the slingshot with a force of for each shot. What value should the width of the rubber band have for the projectile to reach the highest possible velocity? For simplicity, we assume that the elastic energy of the rubber band is completely converted into the kinetic energy of the projectile during firing.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By increasing the width w of the rubber band, the externally applied force is divided to a greater length, so that the rubber band is stretched less. Instead of a rubber band of width w = 4 cm you could also use 4 rubber bands of width w = 1 cm , which are arranged parallel to each other and each experienced only a quarter of the applied force. The general force-distance curve is therefore f n ( w ) = w 1 w f 1 ( x ) = n ⋅ f 1 ( x ) with the force f 1 ( x ) of rubber band of width w 1 = 1 cm and the ratio n = w / w 1 . These force curves are outlined in the diagram below for the cases n = 1 , 2 , 3 and 4. To find out the maximum tensile length x n of the rubber band when the band is loaded with the force f max , we draw the horizontal in the diagram and graphically determine the points of intersection with f n ( x n ) = f max . This yields: x 1 x 2 x 3 x 4 = 1 m , ≈ 0 . 8 5 5 m , ≈ 0 . 7 4 3 m , ≈ 0 . 5 8 8 m In order to determine the elastic energy stored in the rubber, we must integrate the force f ( x ) over the displacement: U n ( x ) ⇒ W 1 W 2 W 3 W 4 = − ∫ 0 x f n ( x ) d x = − n ∫ 0 x f 1 ( x ) d x = n ( 7 5 m 2 J ⋅ x 2 − 7 5 m 4 J ⋅ x 4 + 6 0 m 6 J ⋅ x 6 ) = U 1 ( x 1 ) ≈ 6 0 J , = U 2 ( x 2 ) ≈ 7 6 . 3 J , = U 3 ( x 3 ) ≈ 8 6 J , = U 4 ( x 4 ) ≈ 7 7 . 7 J Because the rubber band with w = 3 cm stores the largest elastic energy, the fired ball in this case receives the highest kinetic energy and therefore the highest speed.