Rubber Physics (Part 4)
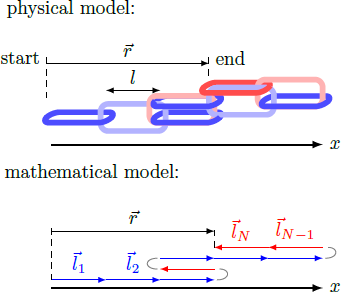
Imagine a chain of chain links aligned parallel to the -axis. Each individual chain link has length and can be aligned either to the right in the direction (blue links) or to the left in the direction (red links). In each case, we associate with the chain link a direction vector whose sign identifies the orientation of the link. The distance vector from start to end of the chain is Let us assume that the alignment of the chain links is purely random and uncorrelated. The probabilities for the alignment of a chain link to the left and right are the same.
What is mean value of the distance between the start and end of the chain? Evaluate for the case and give the result in units of .
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Instead of the distance vector r consider the number n = l r ⋅ e x = l 1 i = 1 ∑ N l i ⋅ e x = i = 1 ∑ N s i ∈ Z with the sign s i ∈ { + 1 , − 1 } of the orientation vector l i = s i l e x . This number can be expressed by n = N + − N − = 2 N + − N with the number of positive vectors, N + , and the number of negative vectors, N − = N − N + . The probability that there are exactly N + positive orientated chain links correspond to a binomial distribution: P N ( N + ) = N + ! ( N − N + ) ! N ! p + N + p − N − N + = ( N N + ) p + N + p − N − N + with probabilites p + and p − = 1 − p + for the cases s i = + 1 and s i = − 1 , respectively. Here, both probabilities are the same, so that p + = p − = 2 1 . The mean value of the quatratic distance results ⟨ r 2 ⟩ = ⟨ n 2 ⟩ l 2 = ( 4 ⟨ N + 2 ⟩ − 4 ⟨ N + ⟩ N + N 2 ) l 2 These mean values ⟨ N + ⟩ and ⟨ N + 2 ⟩ can be estimated as follows ⟨ N + ⟩ ⟨ N + 2 ⟩ = N + = 0 ∑ N N + P N ( N + ) = N + = 0 ∑ N N + N + ! ( N − N + ) ! N ! p + N + p − N − N + = N + = 1 ∑ N ( N + − 1 ) ! ( N − N + ) ! N ! p + N + p − N − N + = N + = 1 ∑ N N p + ⋅ ( N + − 1 ) ! ( ( N − 1 ) − ( N + − 1 ) ) ! ( N − 1 ) ! p + N + − 1 p − ( N − 1 ) − ( N + − 1 ) = N p + N + ′ = 0 ∑ N − 1 N + ′ ! ( ( N − 1 ) − N + ′ ) ! ( N − 1 ) ! p + N + ′ p − ( N − 1 ) − N + ′ = N p + N + ′ = 0 ∑ N − 1 P N − 1 ( N + ′ ) = N p + = N + = 0 ∑ N N + 2 P N ( N + ) = N + = 0 ∑ N N + ( N + − 1 ) P N ( N + ) + N + = 0 ∑ N N + P N ( N + ) = N + = 0 ∑ N N + ( N + − 1 ) N + ! ( N − N + ) ! N ! p + N + p − N − N + + ⟨ N + ⟩ = N + = 2 ∑ N ( N + − 2 ) ! ( N − N + ) ! N ! p + N + p − N − N + + N p + = N + = 2 ∑ N N ( N − 1 ) p + 2 ( N + − 2 ) ! ( ( N − 2 ) − ( N + − 2 ) ) ! ( N − 2 ) ! p + N + − 2 p − ( N − 2 ) − ( N + − 2 ) + N p + = N ( N − 1 ) p + 2 N + ′ = 0 ∑ N − 2 N + ′ ! ( ( N − 2 ) − N + ′ ) ! ( N − 2 ) ! p + N + ′ p − ( N − 2 ) − N + ′ + N p + = N ( N − 1 ) p + 2 N + ′ = 0 ∑ N − 2 P N − 2 ( N + ′ ) + N p + = N ( N − 1 ) p + 2 + N p + Therefore, we get the final result ⟨ r 2 ⟩ = ( 4 ( N ( N − 1 ) p + 2 + N p + ) − 4 N 2 p + + N 2 ) l 2 = ( 4 N ( N − 1 ) ( p + 2 − p + ) + N 2 ) l 2 = ( 4 N ( N − 1 ) ( 4 1 − 2 1 ) + N 2 ) l 2 = ( − N ( N − 1 ) + N 2 ) l 2 = N l 2 ⇒ r m = ⟨ r 2 ⟩ = N ⋅ l = 1 0 0 ⋅ l