Rubber Physics (Part 5)

Classical Mechanics Level 4

We refer back to the model of a one-dimensional chain from part 4 .

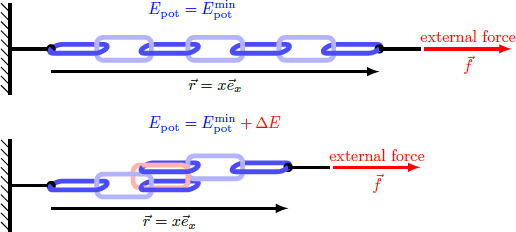
The chain consists of N N chain links, each having a length of l . l. This time we assume that the first chain link is fixed, while on the end of the chain a force of f ⃗ = f e ⃗ x \vec f = f \vec e_x acts. The outer force aligns the chain links in the + x +x direction so that the chain assumes its minimum potential energy when extended to its maximum length r ⃗ = N l e ⃗ x . \vec r = N l \, \vec e_x.

How much energy Δ E \Delta E does it take to flip a single chain link in the opposite direction?

Δ E = − N l f \Delta E = -N l f Δ E = − 2 l f \Delta E = -2 l f Δ E = − l f \Delta E = -l f Δ E = l f \Delta E = l f Δ E = 2 l f \Delta E = 2 l f Δ E = N l f \Delta E = N l f

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Markus Michelmann
Jan 13, 2018

The potential energy of the chain depends linear on the distance vector r ⃗ = x e ⃗ x \vec r = x \vec e_x : E pot = − r ⃗ ⋅ f ⃗ = − ∑ i = 1 N l ⃗ i ⋅ f ⃗ = − ∑ i = 1 N s i l f E_\text{pot} = - \vec r \cdot \vec f = - \sum_{i=1}^N \vec l_i \cdot \vec f = - \sum_{i = 1}^N s_i l f with the orientation vectors of the chain links, l ⃗ i = s i l e ⃗ x \vec l_i = s_i l \vec e_x , and the corresponding sign, s i = ± 1 s_i = \pm 1 . If all signs s i s_i are positive, the potential energy takes the value E pot = E pot min = − N l f E_\text{pot} = E_\text{pot}^\text{min} = - N l f If we flip a sigle chain link, we get E pot = − ( N − 1 ) l f + N l f = − N l f + 2 l f = E pot min + Δ E ⇒ Δ E = 2 l f \begin{aligned} E_\text{pot} &= -(N-1) l f + N l f = - N l f + 2 l f \\ &= E_\text{pot}^\text{min} + \Delta E \\ \Rightarrow \quad \Delta E &= 2 l f \end{aligned}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...