Rubber Physics (Part 6)
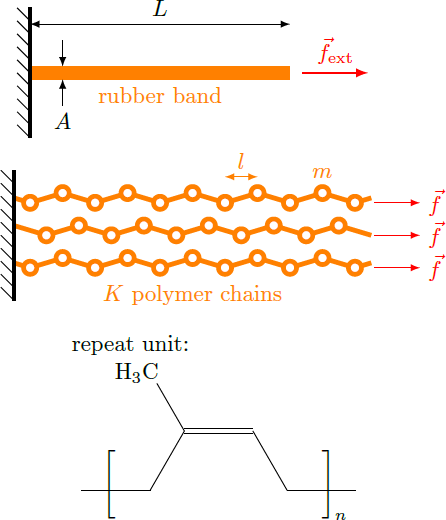
Instead of a single, one-dimensional chain we now consider a macroscopic rubber band with the length and the cross-sectional area , on which an external force acts. We assume that the rubber is composed of a number of polymer chains, which are aligned parallel to the x-axis and on each of which a force acts. The polymer chains consist of individual units, each having a length and a mass . The chemical empirical formula of such a repeat unit is C H . Each of these units represents a chain link of a one-dimensional chain, which may be either parallel or anti-parallel to the external force. Let be the energy needed to flip a single chain link, that we have estimated in part 5 . Estimate for this case the energy ratio where is the Boltzmann constant and is the room temperature in Kelvin.
Details: Rubber has a density of . Hydrogen and carbon atoms each have an atomic weight of and with the atomic mass unit .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The rubber band has a volume V = A L and a mass M = K N m with the number, K , of polymer chains and the number, N = L / l , of chain elements per polymer. The mass of an repeat unit is m = 8 ⋅ m H + 5 ⋅ m C ≈ 1 . 1 3 ⋅ 1 0 − 2 5 kg . The density thus results ρ = V M = A l K m ⇒ K = m A l ρ The force on a single polymer chain is the fraction f = f ext / K of external force. The excitation energy results Δ E = 2 l f as shown in the last problem. Therefore, the energy ratio yields k B T Δ E = K k B T 2 l f ext = A ρ k B T 2 m f ext ≈ ( 3 ⋅ 1 0 − 6 m 2 ) ⋅ ( 9 5 0 kg / m 3 ) ⋅ ( 1 . 3 8 ⋅ 1 0 − 2 3 J / K ) ⋅ ( 2 9 3 K ) 2 ⋅ ( 1 . 1 3 ⋅ 1 0 − 2 5 kg ) ⋅ ( 1 0 N ) ≈ 0 . 2 Thus, the thermal energy k B T and the excitation energy Δ E have a comparable order of magnitude, so that the flipping of individual chain links in the rubber can be excited by the thermal movement. Although the external force energetically favors parallel alignment of all the chain elements, the thermal motion causes the chain elements to flip randomly so that the polymer chains are only partially unraveled and have only a fraction of their actual length.